(Deadline: -)
Daca nu sunteti logati exercitiile nu se mai afiseaza.
Grafuri
Grafuri neorientate
Un graf neorientat, G, este o pereche de multimi (N,M), un de N este o multime finita de noduri (entitati/obiecte continand informatie) si M o multime finita de muchii (legaturi/relatii intre doua noduri) avand elementele sub forma de perechi neordonate de noduri. Nodurile se mai intalnesc si cu denumirea de varfuri.
Adesea in reprezentarea grafurilor, nodurile au asociat un identificator (de cele mai multe ori numeric: nodul 1, nodul 2, etc.).
Exemple de grafuri neorientate:
Grafuri orientate
Un graf orientat G este o pereche de multimi (N,A), unde N e o multime finita de noduri, iar A este o multime de arce ( legaturi orientate intre doua varfuri) avand elementele sub forma de perechi ordonate de noduri.
Exemple de grafuri orientate:
Ce tip de graf este cel mai bun pentru a simula:
- o retea de strazi (de exemplu daca dorim sa calculam cel mai scurt drum pentru un om care vrea sa ajunga din locatia A in locatia B)
- vasele de sange ale corpului uman (de exemplu avem un mic robot care se deplaseaza prin corp incercas sa plaseze un cateter
- o retea de calculatoare (de exemplu daca vrem sa urmarim drumul unui mesaj transmis de la un claculator la altul)
- retele telefonice (ne gandim la centrala, utilizatori)
- o cladire (camerele sunt nodurile, muchiile reprezinta trecerile directe dintr-o camera intr-alta/ usile)
- un rau cu afluentii sai (daca vrem sa aflam pentru o nava daca poate ajunge de la o locatie A la o locatie B)
- un labirint
- relatiile de pritenie dintr-un grup de persoane
- sistemele de tunele, pesterile, minele
Metode de reprezentare a grafurilor:
Vom vedea mai jos mai multe moduri de reprezentare pentru graful neorientat:
![[imagine graf neorientat]](./imagini/grafNeorientat4noduri.png)
si pentru graful orientat:
![[imagine graf orientat]](./imagini/grafOrientat4noduri.png)
Matrice de adiacenta
Intr-o matrice de adicenta vom avea numarul de linii si de coloane egal cu numarul de noduri. Nodului i ii corespunde atat linia i cat si coloana i. Avem proprietatea ca m[i][j] = 1 daca avem conexiune intre nodul i si nodul j si 0 altfel.
Observatie: pe diagonala avem intotdeauna valoarea 0.
Pentru grafurile neorientate, matricea de adicenta este simetrica, pentru cele orientate, nu e obligatoriu sa fie.
Reamintim definirea unei matrici in Python (sub forma unei liste de liste):
m=[
Putem spune cu siguranta ca matricea de mai sus este a unui graf neorientat?
[0,1,1,1],
[1,0,0,1],
[1,0,0,0],
[1,1,0,0],
]
Vector de noduri si de muchii
In cod se specifica, asa cum avem si in definitie, multimea de noduri si de muchii.
graf={
Daca stim ca e graf neorientat, putem sa nu mai specificam muchiile in ambele sensuri (adica si sub forma (a,b) si sub forma (b,a)), dar va trebui sa avem grija in programe sa testam ambele capete.
"noduri": [1,2,3,4],
"muchii": [(1,2), (1,3), (1,4), (2,1), (2,4), (3,1),(4,1),(4,2)]
}
graf={
"noduri": [1,2,3,4],
"muchii": [(1,2), (1,3), (1,4), (2,4)]
}
liste de vecini
Pentru fiecare nod din graf se da o lista cu nodurile catre care pornesc muchii/arce din nodul curent
graf={
1: [2,3,4],
2: [1, 4],
3: [1],
4: [1, 2]
}
Observatie: Pentru un nod din care nu pornesc arce/muchii se va trece lista vida.
![[graf cu nod izolat]](./imagini/grafNeorientat_nodIzolat.png)
graf={
1: [2,3],
2: [1, 3, 5],
3: [1],
4: [1, 2]
}
Termeni asociati grafurilor
Grafuri neorientate:
Vom exemplifica termenii pe graful G din imagine:
![[graf neorientat cu 7 noduri]](./imagini/grafNeorientat7noduri.png)
- Lant
-
un sir ordonat de noduri dintre care oricare doua noduri de pe pozitii consecutive sunt capete ale unei muchii din graf. De exemplu, in graful G formeaza un lant nodurile 1,4,5,6:
![[graf neorientat cu 7 noduri in care e marcat un lant]](./imagini/grafNeorientat7noduriLant1.png)
Un alt exemplu de lant este 7,1,4,5,6,1,3. Chiar si 1,7 este un lant. - Lant elementar
- Un lant in care nodurile sunt distincte doua cate doua (nu avem doua noduri identice in lant).
De exemplu, 1,4,5,6 este lant elementar. - Lant neelementar
- un lant care nu este elementar 😊. De exemplu, lantul 7,1,4,5,6,1,3 este neelementar.
- Lant simplu
- un lant in care nu se repeta nicio muchie. De exemplu, atat 1,4,5,6 cat si 7,1,4,5,6,1,3 sunt simple.
- Lant compus
- un lant care nu este simplu 😊. De exemplu, lantul 1,2,4,1,2 este compus.
- Ciclu
- multime ordonata de noduri dintre care oricare doua noduri de pe pozitii consecutive sunt capete ale unei muchii din graf si in plus, exista o muchie intre primul si ultimul nod. De exemplu, in graful de mai jos formeaza un ciclu.
- Lungimea unui lant (respectiv a unui ciclu)
- numarul de muchii din componenta lui. De exemplu, 1,4,5,6 are lungime 3.
- Ciclu elementar
- Un ciclu in care nodurile sunt distincte doua cate doua (nu avem doua noduri identice in ciclu).
De exemplu, 1,2,4,1 este ciclu elementar:
![[graf neorientat cu 7 noduri in care e marcat un ciclu elementar]](./imagini/grafNeorientat7noduriCiclu1.png)
- Lant sau ciclu elementar de lungime maxima
-
Un lant/ciclu elementar de lungime L cu proprietatea ca nu exista un lant/ciclu elementar de lungime mai mare decat L.
In imaginea de mai jos, 7,1,2,4,5,6 este un lant elementar de lungime maxima (lungimea fiind 5):
![[graf neorientat cu 7 noduri in care e marcat un ciclu elementar de lungime maxima]](./imagini/grafNeorientat7noduriCicluMax.png)
Nu este singurul lant de lungime maxima. Un alt exemplu este: 3,1,2,4,5,6.
In imaginea de mai jos, 1,2,4,5,6,1 este un ciclu elementar de lungime maxima (lungimea fiind 5):
![[graf neorientat cu 7 noduri in care e marcat un ciclu elementar de lungime maxima]](./imagini/grafNeorientat7noduriCicluMax.png)
- Drum
- multime ordonata de noduri dintre care pentru orice pereche de doua noduri de pe pozitii consecutive avem un arc care porneste din primul nod din pereche catre al doilea nod din pereche. De exemplu, 1,2,4,6,5 in graful G formeaza un drum.
- Circuit
- multime ordonata de noduri dintre care oricare doua noduri de pe pozitii consecutive sunt capete ale unei muchii din graf si in plus, exista o muchie intre primul si ultimul nod. De exemplu, 1,2,4,3 in graful G formeaza un circuit.
Grafuri orientate:
Vom exemplifica termenii pe graful G din imagine:
![[graf orientat cu 7 noduri]](./imagini/grafOrientat7noduri.png)
Grafuri cu muchii/arce ponderate
- Grafuri cu muchii ponderate - grafuri care au asociata o pondere (numar real) pentru fiecare muchie
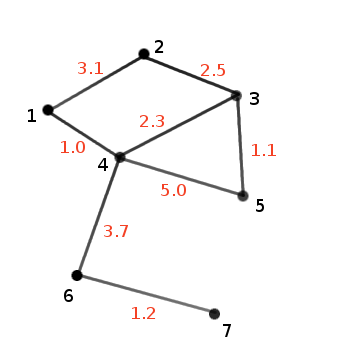
Pentru un graf cu muchii ponderate vom memora si ponderile in reprezentarea sa
-
Matrice de ponderi:
0.0 3.1 0.0 1.0 0.0 0.0 0.0
3.1 0.0 2.5 0.0 0.0 0.0 0.0
0.0 2.5 0.0 2.3 1.1 0.0 0.0
1.0 0.0 2.3 0.0 5.0 3.7 0.0
0.0 0.0 1.1 5.0 0.0 0.0 0.0
0.0 0.0 0.0 3.7 0.0 0.0 1.2
0.0 0.0 0.0 0.0 0.0 1.2 0.0
- lista de noduri si de muchii
- liste de vecini
Arbori
Un arbore neorientat este un graf neorientat conex si fara cicluri.
Un arbore orientat este un graf orientat conex si fara circuite.
Numim radacina un nod special ales in graf. Nodurile catre care pornesc arce/muchii din radacina se numesc fii/copii ai acesteia. Pentru aceste noduri radacina e considerata nod-parinte. Aceasta relatie se propaga spre nodurile urmatoare astfel: nodurile care sunt unite prin muchii/arce de catre nodul curent, si nu reprezinta nodul radacina.
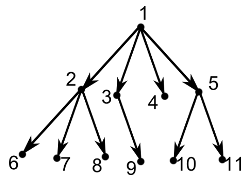
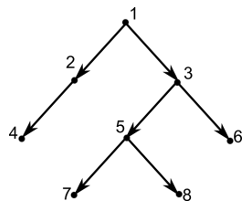
Un arbore binar este un arbore in care fiecare nod are exact doi fii.
Exercitii
Exercitiile se afiseaza doar daca sunteti logati!