Laboratoare inteligenta artificiala

(Deadline: -)

Daca nu sunteti logati exercitiile nu se mai afiseaza.

Tema 1 - cautare informata - Comparație între tehnicile de căutare

Observatie: in cazul in care pentru un tip de mutare nu se precizeaza in mod clar costul, se va considera costul 1.

Observatie: Pe lângă program se va uploada și o documentație în format pdf cu informațiile cerute mai jos. Se poate face și în Google docs punând linkul către ea într-un comentariu pe primul rând al programului

Barem comun

Linkuri utile

https://repl.it/@IrinaCiocan/cautare-BFDFDFI-complet#main.py
https://repl.it/@IrinaCiocan/uniform-cost-search#main.py
https://repl.it/@IrinaCiocan/a-star#main.py
https://replit.com/@IrinaCiocan/a-star-optimizat#main.py
https://replit.com/@IrinaCiocan/ida-star#main.py
https://repl.it/@IrinaCiocan/problemablocurilor#main.py (E implementat cu BF si A*)
https://replit.com/@IrinaCiocan/8-puzzle#main.py
https://repl.it/@IrinaCiocan/exemplu-afisare-timp-folosit (cum calculam timpul de executie a unei secvente de cod)
https://repl.it/@IrinaCiocan/problema-canibalilor-si-misionarilor#main.py
https://repl.it/@IrinaCiocan/exemplu-iterare-prin-folder
http://irinaciocan.ro/inteligenta_artificiala/python-comprehensions.php la secțiunea cu argumentele programului, respectiv timeout
http://irinaciocan.ro/inteligenta_artificiala/cum-rezolvam-o-problema.php modul general de abordare a unei probleme

Barem (punctajul e dat in procentaje din punctajul maxim al temei; procentajul maxim este 100%):

(5%)Fișierele de input vor fi într-un folder a cărui cale va fi dată în linia de comanda. În linia de comandă se va da și calea pentru un folder de output în care programul va crea pentru fiecare fișier de input, fișierul sau fișierele cu rezultatele. Tot în linia de comandă se va da ca parametru și numărul de soluții de calculat (de exemplu, vrem primele NSOL=4 soluții returnate de fiecare algoritm). Ultimul parametru va fi timpul de timeout. Se va descrie în documentație forma în care se apelează programul, plus 1-2 exemple de apel.
(5%) Citirea din fisier + memorarea starii. Parsarea fișierului de input care respectă formatul cerut în enunț
(15%) Functia de generare a succesorilor
(5%) Calcularea costului pentru o mutare
(5%) Testarea ajungerii în starea scop (indicat ar fi printr-o funcție de testare a scopului). Atenție, acolo unde nu se precizează clar în fișierul de intrare o stare finală înseamnă că funcția de testare a scopului doar verifică niște condiții precizate în enunț. Nu se va rezolva generând toate stările finale posibile fiindca e ineficient, ci se va verifica daca o stare curentă se potrivește descrierii unei stări scop.
(15% = 2+5+5+3 ) 4 euristici:
- (2%) banala
- (5%+5%) doua euristici admisibile posibile (se va justifica la prezentare si in documentație de ce sunt admisibile)
- (3%) o euristică neadmisibilă (se va da un exemplu prin care se demonstrează că nu e admisibilă). Atenție, euristica neadmisibilă trebuie să depindă de stare (să se calculeze în funcție de valori care descriu starea pentru care e calculată euristica).
(10%) crearea a 4 fisiere de input cu urmatoarele proprietati:
1. un fisier de input care nu are solutii
2. un fisier de input care da o stare initiala care este si finala (daca acest lucru nu e realizabil pentru problema, aleasa, veti mentiona acest lucru, explicand si motivul).
3. un fisier de input care nu blochează pe niciun algoritm și să aibă ca soluții drumuri lungime micuță (ca să fie ușor de urmărit), să zicem de lungime maxim 20.
4. un fisier de input care să blocheze un algoritm la timeout, dar minim un alt algoritm să dea soluție (de exemplu se blochează DF-ul dacă soluțiile sunt cât mai "în dreapta" în arborele de parcurgere)
5. dintre ultimele doua fisiere, cel putin un fisier sa dea drumul de cost minim pentru euristicile admisibile si un drum care nu e de cost minim pentru cea euristica neadmisibila
(15%) Pentru cele NSOL drumuri(soluții) returnate de fiecare algoritm (unde NSOL e numarul de soluții dat în linia de comandă) se va afișa:
- numărul de ordine al fiecărui nod din drum
- lungimea drumului
- costului drumului
- timpul de găsire a unei soluții (atenție, pentru soluțiile de la a doua încolo timpul se consideră tot de la începutul execuției algoritmului și nu de la ultima soluție)
- numărul maxim de noduri existente la un moment dat în memorie
- numărul total de noduri calculate (totalul de succesori generati; atenție la DFI și IDA* se adună pentru fiecare iteratie chiar dacă se repetă generarea arborelui, nodurile se vor contoriza de fiecare dată afișându-se totalul pe toate iterațiile
- între două soluții de va scrie un separator, sau soluțiile se vor scrie în fișiere diferite.
Obținerea soluțiilor se va face cu ajutorul fiecăruia dintre algoritmii studiați:
- Pentru studenții de la seria CTI problema se va rula cu algoritmii: BF, DF, DFI, UCS, A* (varianta care dă toate drumurile), A* optimizat (cu listele open și closed, care dă doar drumul de cost minim), IDA*.
- Pentru studenții din seriile Mate-Info și Informatică, problema se va rula cu algoritmii: BF, DF, DFI, A* (varianta care dă toate drumurile), A* optimizat (cu listele open și closed, care dă doar drumul de cost minim), IDA*.
Pentru toate variantele de A* (cel care oferă toate drumurile, cel optimizat pentru o singură soluție, și IDA*) se va rezolva problema cu fiecare dintre euristici. Fiecare din algoritmi va fi rulat cu timeout, si se va opri daca depășește acel timeout (necesar în special pentru fișierul fără soluții unde ajunge să facă tot arborele, sau pentru DF în cazul soluțiilor aflate foarte în dreapta în arborele de parcurgere).
(5%) Afisarea in fisierele de output in formatul cerut
(5%+5%) Validări și optimizari. Veți implementa elementele de mai jos care se potrivesc cu varianta de temă alocată vouă:
- Validare: verificarea corectitudinii datelor de intrare
- Validare: găsirea unui mod de a realiza din starea initială că problema nu are soluții. Validările și optimizările se vor descrie pe scurt în documentație.
- Optimizare: găsirea unui mod de reprezentare a stării, cât mai eficient
- Optimizare: găsirea unor condiții din care sa reiasă că o stare nu are cum sa contina in subarborele de succesori o stare finala deci nu mai merita expandata (nu are cum să se ajungă prin starea respectivă la o stare scop).
- Optimizare: implementarea eficientă a algoritmilor cu care se rulează programul, folosind eventual module care oferă structuri de date performante.
(5%) Comentarii pentru clasele și funcțiile adăugate de voi în program (dacă folosiți scheletul de cod dat la laborator, nu e nevoie sa comentați și clasele existente). Comentariile pentru funcții trebuie să respecte un stil consacrat prin care se precizează tipul și rolurile parametrilor, căt și valoarea returnată (de exemplu, reStructured text sau Google python docstrings).
(5%) Documentație cuprinzând explicarea euristicilor folosite. În cazul euristicilor admisibile, se va dovedi că sunt admisibile. În cazul euristicii neadmisibile, se va găsi un exemplu de stare dintr-un drum dat, pentru care h-ul estimat este mai mare decât h-ul real. Se va crea un tabel în documentație cuprinzând informațiile afișate pentru fiecare algoritm (lungimea și costul drumului, numărul maxim de noduri existente la un moment dat în memorie, numărul total de noduri). Pentru variantele de A* vor fi mai multe coloane în tabelul din documentație: câte o coloană pentru fiecare euristică. Tabelul va conține datele pentru minim 2 fișiere de input, printre care și fișierul de input care dă drum diferit pentru euristica neadmisibilă. În caz că nu se găsește cu euristica neadmisibilă un prim drum care să nu fie de cost minim, se acceptă și cazul în care cu euristica neadmisibilă se obțin drumurile în altă ordine decât crescătoare după cost, adică diferența să se vadă abia la drumul cu numărul K, K>1). Se va realiza sub tabel o comparație între algoritmi și soluțiile returnate, pe baza datelor din tabel, precizând și care algoritm e mai eficient în funcție de situație. Se vor indica pe baza tabelului ce dezavantaje are fiecare algoritm.
Doar pentru studenții de la seria CTI (Bonus 10%) pentru implementarea Greedy și analizarea acestuia împreună cu ceilalți algoritmi.
Doar pentru studenții de la seria CTI (Bonus 10%) pentru fiecare dintre următoarele optimizări pentru cazul în care se cere o singură soluție (deci în program veți avea un if care verifică dacă numărul inițial de soluții cerut era 1):

la BF să se returneze drumul imediat ce nodul scop a fost descoperit, și nu neapărat când ajunge primul în coadă

la UCS+A* (bonusul ar fi 10%+10% dacă se face pt ambele) să nu avem duplicate ale informației din noduri în coadă. În cazul în care tocmai dorim să adăugăm un nod în coadă și vedem că există informația lui deja, păstram în coadă, dintre cele 2 noduri doar pe cel cu costul cel mai mic
Bonus (5%) Dacă faceți mai multe euristici admisibile dar diferite ca idee (cu alt mod de abordare a calculării).
(Bonus 5%) implementare proprie (rescriere completă față de exemplele de la laborator)
(Bonus 15-20%) Adăugarea unei interfețe grafice care să simuleze drumul cu ajutorul unei animații (de exemplu, făcută în pygame).

Tema nu se puncteaza fara prezentare. Se va da o nota pe prezentare de la 1 la 10 in functie de cat de bine a stiut studentul sa explice ce a facut. Punctajul temei se va inmulti cu nota_prezentare/10. Astfel, daca cineva stie sa explice doar jumatate din ce a facut, primeste jumatate din punctaj; daca nu stie nimic primeste 0.

Temele copiate duc la anularea notei atat pentru cel care a dat tema cat si pentru cel care a copiat, iar numele studentilor cu aceasta problema vor fi comunicate profesorului titular de curs.

Problema de cautare (un mesaj...)

Context

In drum spre scoala un copilas a auzit doi copii mai mari vorbind despre un coleg si prieten bun de-al lui. Cei doi vroiau sa-i faca o farsa rautacioasa in prima pauza. Copilasul insa a ajuns dupa ce incepuse ora si a trebuit sa se aseze direct in banca fara a-si putea avertiza colegul de primejdie. Din fericire i-a venit in minte sa-i trimita din coleg in coleg un bilet cu un mesaj in care sa-l atentioneze despre farsa.
Copii sunt asezati in banci de cate doua persoane. Bancile sunt dispuse in K coloane astfel (exemplul pentru K=3):



...



...



...

Un copil poate da fara probleme biletul catre colegul de banca, la fel neobservat de catre profesor poate da biletul catre colegii din fata sau din spatele lui, insa nu si in diagonala, deoarece, intinzandu-se peste banca ar atrage privirea profesorului.

Considerand fragmentul de clasa de mai jos:

a	b
c	d

Elevul a poate trimite biletul doar catre b sau c.

Probleme apar din faptul ca unele locuri in banci pot fi libere, dar si din faptul ca o serie de colegi sunt suparati intre ei si nu-si vorbesc, deci nici nu ar trimite biletul (supararea este reciproca).
De asemenea, trecerea biletelului de pe un rand pe altul este mai anevoioasa, deoarece poate fi vazut foarte usor de catre profesor, de aceea singurele banci intre care se poate face transferul sunt penultimele si ultimele de pe fiecare rand.

În plus profesorul are o listă de elevi pe care îi ascultă în acea zi. Copiii sunt ascultați la lecție în ordinea din listă. O ascultare durează cât M mutări de bilet. Când profesorul ascultă un elev, se află lângă el, așa că biletul nu are voie să fie lângă acel copil (nici în banca sa, sau în cea din față ori din spate, dar nici în bancile din coloanele vecine (care se află la aceeași poziție cu banca elevului ascultat, ori cu o poziție în față, ori o poziție în spate.

Copilul vrea sa scrie pe bilet drumul pe care trebuie sa-l parcurga, de la un coleg la altul, pentru a fi sigur ca nu se rataceste prin clasa si nu mai ajunge la prietenul sau pana la inceputul pauzei.

Se considera prin conventie ca:

fiecare copil este identificat unic prin numele sau.
niciun copil nu se numeste 'suparati' sau 'liber'
locurile libere sunt marcate prin identificatorul 'liber'

Stări și tranziții. Cost.

O stare e dată de poziția biletului și cine e ascultat de profesor la acel moment. Dacă biletul nu a ajuns la destinație și profesorul a terminat de ascultat, înseamnă că nu vor mai exista restricții de mutare legate de acest aspect. Costul unei mutări de bilet în aceeași bancă e 0, între bănci consecutive e 1 și între coloanele de bănci e 2.

Fisierul de intrare

Formatul fisierului de intrare este urmatorul. Pe primele linii din fisier se precizeaza asezarea in banci. Fiecare linie cuprinde 2*K nume (numele sunt formate doar din litere). Primii doi identificatori corespund primei coloane de banci, urmatorii doi identificatori coloanei din mijloc, si utltimii doi, ultimei coloane de banci.

Dupa ce se termina liniile cu asezare in banci, apare un rand cu identificatorul suparati. Sub acest rand, sunt trecuti cate doi elevi (numele lor) care sunt suparati intre ei. Dedesubt e identificatorul "ascultati:", urmat de numărul M, și apoi sunt enumerați copiii ascultați.

Exemplu de fisier: ionel alina teo eliza carmen monica george diana bob liber nadia mihai liber costin anda bogdan dora marin luiza simona dana cristian tamara dragos mihnea razvan radu patricia gigel elena liber andrei oana victor liber dorel viorel alex ela nicoleta maria gabi suparati george ionel ela nicoleta victor oana teo eliza teo luiza elena dragos alina dragos ascultati: 4 monica maria mesaj: ionel -> dragos

Fișier output.

Exemplu de drum din fisierul de iesire: ionel > alina v diana v costin v simona v razvan v andrei >> oana ^ radu > patricia v victor v nicoleta >> maria > gabi ^ dorel ^ elena < gigel ^ tamara > dragos

In urma rularii se va afisa drumul parcurs, in ordine cronologica. Daca biletelul merge in cadrul aceluiasi rand, deci catre un coleg de banca, in stanga, se va afisa <, daca merge in dreapta, se va afisa >. Daca biletelul merge spre spatele clasei, intre copiii care transmit biletul se va afisa un v (pe post de sagetica in jos), iar daca merge spre fata clasei, se va afisa ^ pe post de sagetica in sus. Cand biletul se deplaseaza spre stanga de pe o coloană de banci pe alta, se va afisa <<, iar spre dreapta: >>.

Problema vaselor cu apa

Context

Consideram ca avem niste vase cu apa colorata. Despre fiecare vas stim capacitatea maxima si cat lichid contine. Pot exista si vase vide. De asemenea pentru combinatia a doua culori de lichide stim ce culoare rezulta din combinatia lor. Pentru combinatiile de culori neprecizate, inseamna ca nu ne intereseaza rezultatul si desi le putem amesteca (uneori e nevoie sa depozitam apa intr-un vas, ca sa facem loc pentru alte mutari) culoarea rezultata nu va aparea in starea solutie niciodata (puteti considera un identificator special pentru acea culoare, de exemplu "nedefinit"). Evident, apa cu culoare nedefinita nu poate fi folosita pentru a obtine alte culori (apa cu culoare nedefinita, amestecata cu orice rezulta in culoare nedefinita).

Stări și tranziții

Mutările se fac ținând cont de următoarele reguli:

Lichidul dintr-un vas nu poate fi varsat decat in alt vas (nu dorim sa pierdem din lichid; nu se varsa in exterior).
Indiferent de cantitatea de lichid turnată și cea existentă in vas, culoarea rezultată în vasul în care s-a turnat apa e fie e culoarea indicată în fișierul de intrare pentru combinarea celor două culori, fie nedefinită dacă nu se specifică în fișîerul de intrare rezultatul unei astfel de combinări. Apa de culoare nedefinită, turnată peste orice altă culoare, va transforma apa din vasul în care se toarnă în apă de culoare nedefinită
Apa se poate turna dintr-un vas în altul doar în două moduri: fie se toarnă apă până se golește vasul din care turnăm, fie se umple vasul în care turnăm. Nu se pot turna cantități intermediare.

Costul

Costul turnării este dat de cati litri de o anumită culoare au fost turnați înmulțit cu costul culorii respective. în cazul în care rezultatul turnării este o culoare nedefinită, costul va fi numărul de litri turnați înmulțit cu cât costă un litru din acea culoare, adunat cu numărul de litri din vasul în care se toarnă înmulțit cu costul asociat culorii din el. În cazul în care unul sau ambele vase au deja culoare nedefinită, se consideră cost 1 pentru un litru de culoare nedefinită.

Starea finala (scopul) Considerăm că ajungem în starea finală când obținem cantități fixe (cerute în fișierul de intrare) de apă de o anumită culoare.

Fisierul de intrare

Primele randuri se vor referi la combinatiile de culori. Vor fi cate 3 pe rand, de exemplu: c1 c2 c3 cu semnificatia ca din combinarea culorii c1 cu c2 rezulta c3 (nu conteaza cantitatea apei amestecate ci doar culoarea ei). Combinatiile sunt simetrice, adica, daca din c1 combinat cu c2 rezulta c3, atunci si din c2 combinat cu c1 rezulta c3.

Sub randurile cu culorile avem rânduri cu prețul pe litru al manipulării fiecărei culori. Apoi, un rand cu textul "stare_initiala", dupa care urmeaza starea initiala a vaselor. Pentru fiecare vas se precizeaza cantitatea maxima a acestuia, cata apa are si ce culoare are apa. Toate cantitatile sunt date in litri. In cazul in care cantitatea de apa este 0, lipseste si culoarea. Dupa precizarea starii, initiale, avem textul "stare_finala". Sub acest text pe cate un rand, se specifica o cantitate si o culoare, cu sensul ca in starea finala, pentru fiecare astfel de cantitate (si culoare) precizata trebuie sa existe un vas care sa o contina.

Tranzitia consta din turnarea apei dintr-un vas in altul. Se considera ca nu stim sa masuram litrii altfel decat folosind vasele. Cand turnam lichid putem turna ori pana se termina lichidul din vasul din care turnam, ori pana se umple vasul in care turnam.. Nu se varsa lichid in exterior, lichidul nu da pe afara. Asfel daca, de exemplu, am un vas cu capacitate 6 si cantitate 3 si unul cu capacitate 4 si cantitate 2, nu putem turna din primul doar un litru, ci doar 2 litri (fiindca sunt 4-2=2 litri liberi in vasul al doilea). In felul asta ramanem cu un litru in primul.

Ne oprim din cautat cand reusim sa ajungem in starea finala: cu alte cuvinte, cand fiecare cantitate de apa colorata specificata in stare se gaseste in cate un vas (nu ne intereseaza cantitatile de apa din restul vaselor)

Exemplu de fisier de intrare: rosu albastru mov albastru galben verde mov verde maro rosu 2 albastru 5 mov 7 galben 3 verde 5 maro 4 stare_initiala 5 4 rosu 2 2 galben 3 0 7 3 albastru 1 0 4 3 rosu stare_finala 3 mov 2 verde

Fișier output.

In fisierul de output se vor afisa starile intermediare, pornind de la starea initiala la starea finala. Pentru fiecare vase se aloca un id (poate fi numarul de ordine din fisier - de exemplu, vasul cu id-ul 0 este cel cu capacitate 5 si 4 litri de apa rosie)

O stare se va afisa, afisand intai (daca nu e vorba de prima stare) ce miscare s-a facut, in formatul: Din vasul X s-au turnat L litri de apa de culoare C in vasul Y.

Apoi se va afisa starea vaselor astfel: id_vas: capacitate_maxima cantitate_apa culoare_apa De exemplu, pentru un succesor al starii initiale de mai sus am avea: Din vasul 0 s-au turnat 1 litri de apa de culoare rosu in vasul 4. 0: 5 3 rosu 1: 2 2 galben 2: 3 0 3: 7 3 albastru 4: 1 1 rosu 5: 4 3 rosu Insa starea initiala s-ar fi afisat in drum fara randul cu mutarea: 0: 5 4 rosu 1: 2 2 galben 2: 3 0 3: 7 3 albastru 4: 1 0 5: 4 3 rosu Nu ne preocupam de corectitudine gramaticala ("culoare rosie" in loc de "culoare rosu").

Cand se afiseaza "drumul" de stari, se afiseaza si prima stare in formatul de mai sus (cu id-urile vaselor), dar fara mesajul mutarii.

Un exemplu de distributie a apei intr-o stare finala este (observam ca nu am precizat culoarea pentru cantitate 0): 0: 5 5 rosu 1: 2 1 galben 2: 3 1 albastru 3: 7 2 verde 4: 1 0 5: 4 3 mov Indicatie: nu precizati toate starile finale posibile, ci faceti o functie care testeaza daca o stare indeplineste conditia ceruta.

Alte precizari:

Pentru fisierele de input nu e obligatoriu sa folositi nume reale de culori
Nu e obligatoriu sa se foloseasca toate culorile in starea finala.
În afișarea drumurilor-soluție, se va afișa pentru fiecare nod și indicele stării (nodului) în drum

Micul vrăjitor

Context

Un mic vrajitor a pornit la drum sa gaseasca o piatra magica. Numai ca piatra magica se gaseste intr-o pestera la fel de magica. Pestera e de forma dreptunghiulara impartita in parcele patratice, fiecare de o anumita culoare. La intrarea in pestera un batran vrajitor ii ofera o pereche de cizme de culoarea parcelei care se afla la intrarea in pestera, si il povatuieste sa nu calce niciodata cu o pereche de cizme de o culoare pe o parcela de alta culoare fiindca in mod sigur va muri. Micul vrajitor mai poate sa poarte in desaga o pereche in plus de cizme (o pereche de cizme de rezerva). Batranul de asemenea il atentioneaza ca din cauza energiei terenului vrajit, cizmele se strica dupa 3 parcele parcurse, iar daca nu le schimba pana se strica de tot, va ramane descult in urmatoarea parcela si iar va muri. Unele parcele pot contine o pereche de cizme. Micutul vrajitor poate lua acea pereche de cizme si sa o puna in desaga ori sa-si schimbe cizmele curente pentru intrarea intr-o noua parcela de alta culoare (la schimbarea cizmelor, daca are desaga goala le va pune pe cele vechi in desaga, altfel are de ales intre a le arunca pe acestea ori a le arunca pe cele din desaga si a le pune pe acestea in locul lor). Se considera ca schimbarea cizmelor se face dupa parasirea parcelei curente dar imediat inainte de intrarea intr-o noua parcela (deci sa zicem, intermediar, pe granita - dar nu e nevoie sa considerati granita ca o stare aparte; pasul si scimbarea cizmelor vor fi vazute ca o tranzitie unitara). Micul vrajitor atunci cand are desaga goala va lua intotdeauna cizmele din parcela sa le puna in desaga; de asemenea nu va arunca cizmele din desaga daca nu are altele pe care sa le puna in loc (fie cele incaltate, fie cele gasite in parcela). Insa daca cizmele din desaga sunt de aceeasi culoare cu cele din parcela si sunt nepurtate (numarul de purtari e 0) atunci nu le schimba (nu are de ce, ajunge la 2 stari succesoare posibile identice).

Se considera ca daca au fost luate cizmele dintr-o parcela, dupa plecarea vrajitorului, prin magie apare o noua pereche de aceeasi culoare in acelasi loc (deci daca a luat o pereche de acolo, dar dupa niste pasi a ajuns tot in acea parcela ar gasi o pereche de cizme la fel cu cele luate anterior, si le-ar putea folosi). Nu poate lua insa mai mult de o pereche de cizme dintr-o parcela (adica nu poate sa schimbe si cizmele din desaga si pe cele pe care le avea incaltate cu cele gasite in parcela). Cizmele gasite intr-o parcela sunt intotdeauna noi.

Vrajitorasul tinde spre reinnoirea cizmelor. Daca are in desaga cizme de culoarea celor gasite in parcela, sau poarta cizme de culoarea celor gasite in parcela le va reinnoi daca acestea nu sunt noi deja.

Pentru a nu obtine 2 succesori identici pentru anumite stari, luati in vedere faptul ca nu are sens sa-si schimbe cizmele din desaga cu cele incaltate daca sunt de aceeasi culoare si au acelasi numar de purtari.

La intrarea in pestera se considera ca s-a facut un pas, deci cizmele in starea initiala au numarul de purtari egal cu 1.

Atentie scopul nu e doar sa ajunga la piatra ci si sa iasa cu ea din pestera (intoarcerea la nodul initial). Dupa cum se vede micul vrajitor e supus la grea incercare si numai voi il puteti ajuta sa gaseasca drumul catre piatra magica.

Stări și tranziții. Cost

O stare e dată atât de poziția vrăjitorului cât și de elementele rămase pe hartă. Vrajitorul se poate misca doar pe linie si coloana, nu si pe diagonala. Fiecare deplasare pe un tip de relief are costul său (se adună costul celulei pe care ajunge, nu de pe care pleacă). În plus, se mai poate aduna costul unei schimbări de cizme care este 1.

Fisierul de intrare

Aveti un pic mai jos un exemplu de fisier de intrare. Primele linii conțin costurile pentru deplasarea pe fiecare formă de relief. Urmează un despărțitor și hărțile care sunt doua matrici separate printr-o linie goala. Liniile unei matrici sunt fiecare pe cate un rand nou. Elementele pe linie se separa prin spatii (se poate considera ca fiecare element al matricii e de un singur caracter). Prima matrice reprezinta harta efectiva cu culorile parcelelor. A doua matrice este cea care arata ce obiecte se gasesc in parcelele respective. Tot in a doua matrice e marcat locul de pornire cu un caracter * si locul unde se gaseste pitra cu un @. In parcela de pornire si in cea cu piatra nu aveti si cizme. Daca o parcela nu contine nimic, in matricea a doua va avea alocat un 0 pe pozitia corespunzatoare ei. De exemplu: v 2 r 1 a 3 ---- v r r r v v a v v a a a 0 r a * 0 0 0 0 0 0 @ v

Pentru acest exemplu de fisier de intrare se considera ca se porneste de la coordonatele 0,3 de pe o parcela de culoare r. Piatra se afla la coordonatele 2,2 pe o parcela de culoare a. Parcela de la coordonatele 0,0 este de culoare v si nu contine nimic. Parcela de la coordonatele 0,2 e de culoare r si contine cizme de culoare a.
Desi programul cunoaste harta, se considera ca vrajitorul nu stie cum arata terenul pana nu il descopera singur, mergand prin pestera.

Fișier output.

Fișierul de ieșire va urma modelul de mai jos.

De exemplu pentru fisierul de intrare:

v 2
r 1
a 3
g 2
----
g r v v v v
a r r r r a
a v a r r a
v v a r r a
g g a r r a
v r r g v v
r r a a a a

0 * 0 0 0 0
g a 0 0 0 0
0 r 0 0 0 r
0 0 g 0 0 0
v 0 @ 0 0 0
0 0 0 0 0 g
0 0 0 0 0 0

O solutie posibila e cea de mai jos: (acesta ar fi si continutul fisierului de iesire)

Pas 0). Incepe drumul cu cizme de culoare r din locatia(0,1). Incaltat: r (purtari: 1). Desaga: nimic. Fara piatra.

Pas 1).Paseste din (0,1) in (1,1). Incaltat: r (purtari: 2). Desaga: nimic. Fara piatra.

Pas 2).A gasit cizme a. Schimba cizmele din desaga cu cele din patratel si porneste la drum. Paseste din (1,1) in (1,2). Incaltat: r (purtari: 3). Desaga: a (purtari: 0). Fara piatra.

Pas 3).I s-au tocit cizmele r. Incalta cizmele din desaga si porneste la drum. Paseste din (1,2) in (2,2). Incaltat: a (purtari: 1). Desaga: nimic. Fara piatra.

Pas 4).Paseste din (2,2) in (3,2). Incaltat: a (purtari: 2). Desaga: nimic. Fara piatra.

Pas 5).A gasit cizme g. Schimba cizmele din desaga cu cele din patratel si porneste la drum. Paseste din (3,2) in (4,2). Incaltat: a (purtari: 3). Desaga: g (purtari: 0). Fara piatra.

Pas 6).I s-au tocit cizmele a. Incalta cizmele din desaga ia piatra si porneste la drum. Paseste din (4,2) in (4,1). Incaltat: g (purtari: 1). Desaga: nimic. Cu piatra.

Pas 7).Paseste din (4,1) in (4,0). Incaltat: g (purtari: 2). Desaga: nimic. Cu piatra.

Pas 8).A gasit cizme v. Muta cizmele incaltate in desaga si le incalta pe cele din patratel si porneste la drum. Paseste din (4,0) in (3,0). Incaltat: v (purtari: 1). Desaga: g (purtari: 2). Cu piatra.

Pas 9).Paseste din (3,0) in (3,1). Incaltat: v (purtari: 2). Desaga: g (purtari: 2). Cu piatra.

Pas 10).Paseste din (3,1) in (2,1). Incaltat: v (purtari: 3). Desaga: g (purtari: 2). Cu piatra.

Pas 11).I s-au tocit cizmele v. A gasit cizme r. Incalta aceste cizme si porneste la drum. Paseste din (2,1) in (1,1). Incaltat: r (purtari: 1). Desaga: g (purtari: 2). Cu piatra.

Pas 12).Paseste din (1,1) in (0,1). Incaltat: r (purtari: 2). Desaga: g (purtari: 2). Cu piatra.

A iesit din pestera.

Indicatie: pentru a face usor afisarea (dar si verificarea solutiei) este bine sa aveti in cadrul starii ce defineste un nod si un camp care sa reprezinte cazul prin care a ajuns de la o stare la alta (de exemplu: caz 1 a facut un pas simplu, caz 2 a gasit piatra, caz 3 a incaltat cizmele din desaga etc. pentru a nu fi nevoiti sa comparati starea anterioara cu cea curenta) De exemplu, la mine in program ultimul camp dintr-o structura st reprezinta cazul. Solutia scrisa ca lista este: [(0,1,r,1,0,0,0,0), (1,1,r,2,0,0,0,1), (1,2,r,3,a,0,0,7), (2,2,a,1,0,0,0,12), (3,2,a,2,0,0,0,1), (4,2,a,3,g,0,0,7), (4,1,g,1,0,0,1,9), (4,0,g,2,0,0,1,1), (3,0,v,1,g,2,1,6), (3,1,v,2,g,2,1,1), (2,1,v,3,g,2,1,1), (1,1,r,1,g,2,1,11), (0,1,r,2,g,2,1,1)]
Atentie nu e obligatoriu sa memorati starile neaparat in acest fel; este doar o indicatie; orice mod corect de reprezentare alternativa este acceptat.

Evadarea Broscoceilor...

Context

N broscute mici de tot stateau fiecare pe câte o frunza la fel de mica, și pluteau alene pe suprafata unui lac. Broscutele noastre fiind foarte tinere, încă nu stiau să inoate si nu le placea apa si poate de aceea isi doreau tare mult sa scape din lac si sa ajunga la mal. Singurul mod in care puteau sa realizeze acest lucru era sa sara din frunza in frunza.

Forma lacului poate fi aproximata la un cerc. Coordonatele frunzelor sunt raportate la centrul acestui cerc (deci originea axelor de coordonate, adica punctul (0,0) se afla in centrul cercului).

Broscuțele sar din frunză în frunză. Lungimea unei sarituri de broscuță e maxim valoarea greutatii/3. Din cauza efortului depus, broscuta pierde o unitate de energie(greutate) la fiecare saritura. Se considera ca pierderea in greutate se face in timpul saltului, deci cand ajunge la destinatie are deja cu o unitate mai putin.

Daca o broscuta ajunge la greutatea 0, atunci moare.

Pe unele frunze exista insecte, pe altele nu. Cand broscuta ajunge pe o frunza mananca o parte (un număr între 0 și câte insecte se găsesc pe frunză) din insectele gasite si acest lucru ii da energie pentru noi sărituri. In fisierul de intrare se va specifica numarul de insecte gasite pe fiecare frunza. Daca broscuta mananca o insecta, ea creste in greutate cu o unitate. Atentie, odata ce a mancat o parte din insectele de pe o frunza, frunza ramâne, bineinteles fara acel numar de insecte.

Fiecare frunză are o greutate maximă acceptată. Greutatea de pe o frunză e dată de greutatea insectelor adunată cu cea a broscuțelor (pot fi și mai multe pe o frunză).

Stări și tranziții

Deși vom trata toate salturile ca pe o singură mutare, în realizarea calculelor referitoare la greutăți și insecte vom considera că broscuțele sar în mod ordonat după indicele lor. Totuși nu vom crea câte un nod pentru fiecare broscuță, ci pentru toate salturile în același timp.

O tranzitie e considerata a fi consumarea insectelor de pe frunza pe care se află plus un slat pe altă frunză.

Costul

Costul e dat de distanta totală, parcursă de toate broscuțele până la acel moment.

Fisierul de intrare

Formatul fisierului este: raza_cerc_lac nume_broscuta_0 greutate_broscuta_0 id_frunza_start_0 ... nume_broscuta_n greutate_broscuta_n id_frunza_start_n identificator_frunza_1 x1 y1 nr_insecte_1 greutate_max_1 ... identificator_frunza_n xn yn nr_insecte_n greutate_max_n

De exemplu, pentru fisierul de intrare: 7 Broscovina 5 id1 Mormolocel 3 id12 id0 1 5 3 5 id1 0 0 0 5 id2 -1 1 3 8 id3 0 2 0 7 id4 2 2 3 10 id5 3 0 1 5 id6 -3 1 1 6 id7 -4 1 3 7 id8 -4 0 1 7 id9 -5 0 2 8 id10 -3 -3 4 12 id11 1 -3 3 6 id12 0 -2 2 5 id13 -2 -1 3 9 id14 -1 -1 7 15

Fișierul de intrare de mai sus descrie imaginea (dați click pe ea pentru a o deschide în fereastră nouă):

lac — B0 și B1 indică unde sunt broscuțele (numărul de după B reprezentând indicele lor în enumerație).

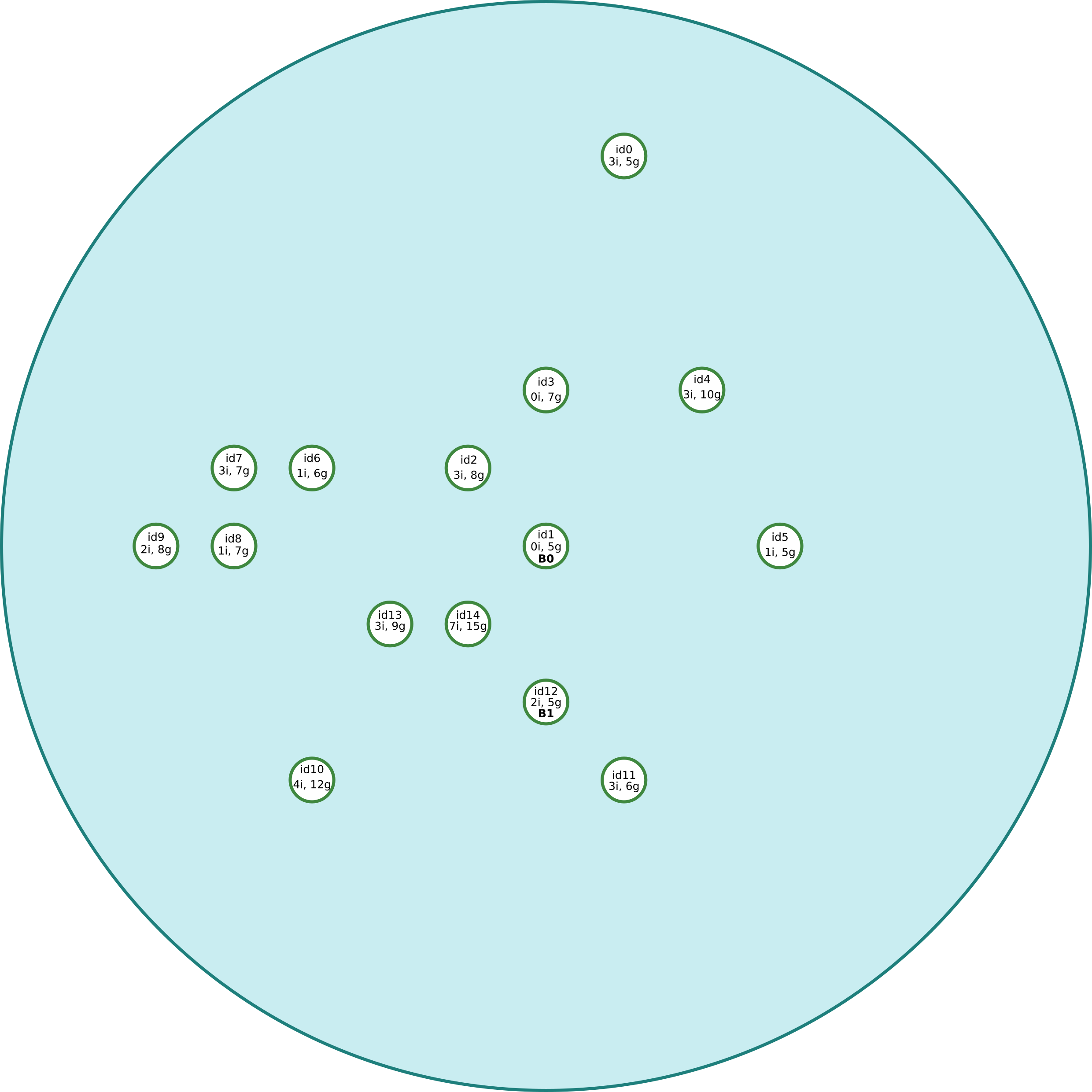
Fișier output.

În fișierul de output se vor afișa drumurile-soluție. Primul nod va avea o afișare specială, fiind vorba de starea inițială: se va indica poziția fiecărei broscuțe, plus stările frunzelor. Starea unei frunze are formatul: [id-frunza]([numar-insecte],[greutate]), unde parantezele drepte sunt înlocuite cu informația cerută. In cadrul afisarii soutiei, pentru fiecare nod din drum se va afișa:

câte insecte au mâncat broscuțele înainte de salt
poziția broscuțelor înainte și după salt
starea frunzelor

Afișarea ar trebui să aibă o formă asemănătoare cu cea de mai jos. Un exemplu de drum (nu neapărat cel de cost minim) este: 0) Broscovina se afla pe frunza initiala id1(0,0). Greutate broscuta: 5 Mormolocel se afla pe frunza initiala id12(0,-2). Greutate broscuta: 3 Stare frunze: id0(3,5), id1(0,5), id2(3,8), id3(0,7), id4(3,10), id5(1,5), id6(1,6), id7(3,7), id8(1,7), id9(2,8), id10(4,12), id11(3,6), id12(2,5), id13(3,9), id14(7,15) 2) Broscovina a mancat 0 insecte. Broscovina a sarit de la id1(0,0) la id14(-1,1). Greutate broscuta: 4. Mormolocel a mancat 2 insecte. Mormolocel a sarit de la id12(0,-2) la id14(-1,1). Greutate broscuta: 4 Stare frunze: id0(3,5), id1(0,5), id2(3,8), id3(0,7), id4(3,10), id5(1,5), id6(1,6), id7(3,7), id8(1,7), id9(2,8), id10(4,12), id11(3,6), id12(0,5), id13(3,9), id14(7,15) 3) Broscovina a mancat 2 insecte. Broscovina a sarit de la id14(-1,1) la id13(-2,1). Greutate broscuta: 5. Mormolocel a mancat 5 insecte. Mormolocel a sarit de la id14(-1,1) la id10(-3,-3). Greutate broscuta: 8 Stare frunze: id0(3,5), id1(0,5), id2(3,8), id3(0,7), id4(3,10), id5(1,5), id6(1,6), id7(3,7), id8(1,7), id9(2,8), id10(4,12), id11(3,6), id12(0,5), id13(3,9), id14(0,15) 4) Broscovina a mancat 2 insecte. Broscovina a sarit de la id13(-2,-1) la id8(-4,0). Greutate broscuta: 6. Mormolocel a mancat 1 insecte. Mormolocel a sarit de la id10(-3,-3) la mal. Greutate broscuta: 8 Stare frunze: id0(3,5), id1(0,5), id2(3,8), id3(0,7), id4(3,10), id5(1,5), id6(1,6), id7(3,7), id8(1,7), id9(2,8), id10(3,12), id11(3,6), id12(0,5), id13(1,9), id14(0,15) 5) Broscovina a mancat 1 insecte. Broscovina a sarit de la id8(-4,0) la id9(-5,0). Greutate broscuta: 6. Stare frunze: id0(3,5), id1(0,5), id2(3,8), id3(0,7), id4(3,10), id5(1,5), id6(1,6), id7(3,7), id8(0,7), id9(2,8), id10(3,12), id11(3,6), id12(0,5), id13(1,9), id14(0,15) 6) Broscovina a mancat 0 insecte. Broscovina a sarit de la id9(-5,0) la mal. Greutate broscuta: 5. Stare frunze: id0(3,5), id1(0,5), id2(3,8), id3(0,7), id4(3,10), id5(1,5), id6(1,6), id7(3,7), id8(0,7), id9(2,8), id10(3,12), id11(3,6), id12(0,5), id13(1,9), id14(0,15)

Observație: greutatea afișată a broscuței este după ce s-a consumat și unitatea pentru salt

Problema unui lacat

Context.

Se considera un lacat cu un numar N de incuietori legate intre ele, puse una in continuarea celeilalte astfel incat cu o cheie speciala se pot accesa toate incuietorile in acelasi timp si se pot incuia/descuia dupa caz. O cheie e impartita pe un numar de zone egal cu numarul de incuietori. O astfel de zona poate incuia descuia sau lasa in aceeasi stare o incuietoare, independent de efectul celorlate portiuni ale cheii asupra celorlalte incuietori. O cheie e codificata printr-o secventa de litere din multimea {d,g,i}, unde d inseamna ca are rolul de a descuia, i are rolul de a incuia iar g e gol, efect nul, lasa incuietoarea corespunzatoare asa cum a gasit-o. O cheie poate fi folosită de maxim K ori înainte de a se strica (nu mai poate fi folosită dacă se strică). O incuietoare poate fi de mai multe ori inchisa, adica, daca a fost incuiata de N ori va trebui sa fie descuiata de N ori ca sa fie deschisa. O incuietoare deja descuiata daca e deschisa de cheie va ramane tot descuiata.
De exemplu daca avem 6 incuietori si primele trei sunt inchise (o data), celelalte 3 deschise si aplicam cheia dgidgi

i1	i1	i1	d	d	d
d	g	i	d	g	i

d	i1	i2	d	d	i1

Initial toate incuietorile sunt inchise o data

Lacătul e un lacăt cu trucuri. Unele încuietori, atunci când se deschid, încuie o altă încuietoare. De exemplu, daca încuietoarea 0 e cu truc, și încuie încuietoarea 4, pentru cazul de mai jos, după aplicarea cheii avem:

i1	i1	i1	d	d	d
d	g	i	d	g	i

d	i1	i2	d	i1	i1

Sau dacă încuietoarea 4 era deja închisă:

i1	i1	i1	d	i1	d
d	g	i	d	g	i

d	i1	i2	i2	i2	i1

Dacă pe poziția 4 în cheie aveam d în loc de g, se anula efectul de închidere:

i1	i1	i1	d	d	d
d	g	i	d	d	i

d	i1	i2	d	i1	i1

Stări și tranziții

Nodurile-stări în graful problemei vor stările diferite ale lacătului. O schimbare de stare se face când folosim o cheie.

Costul

Costul va fi egal cu totalul descuierilor pe toate încuietorile (reamintim ca o încuietoare e una dintre părțile lacătului). O descuiere e fie o decrementare a numărului de încuieri, fie o trecere de la o încuiere la "deschis". Dacă încuietoarea e una cu truc și e încuiata ca efect al descuierii altei încuietori, dar în același timp pe poziția ei cheia are "d", atunci nu se adună la cost (presupunem ca de fapt cheia blochează încuierea)

Fisierul de intrare

Fisierul de intrare cuprinde:

numărul K
încuietorile cu truc, sub forma indice_1->indice_2, cu sensul ca descuierea încuietorii de pe poziția indice_1 duce la încuierea celei de pe poziția indice_2.
codul fiecarei chei in parte sub forma unui termen format din literele d,g,i.

Exemplu de fisier de intrare:

3
2->6
idddgii
idiidid
iidddii
iddgiig
dgggiid
didiigg
gigddgg
gdggggg
gggiggd
dgggddd

Fișier output.

In cadrul afisarii solutiei se va arata la fiecare pas starea incuietorii si cheia folosita.

Exemplu de afisare (nu e neaparat drumul de cost minim): Initial: [inc(i,1),inc(i,1),inc(i,1),inc(i,1),inc(i,1),inc(i,1),inc(i,1)] 1) Incuietori: [inc(i,1),inc(i,1),inc(i,1),inc(i,1),inc(i,1),inc(i,1),inc(i,1)]. Folosim cheia: gdggggg. 2) Incuietori: [inc(i,1),inc(d,0),inc(i,1),inc(i,1),inc(i,1),inc(i,1),inc(i,1)]. Folosim cheia: dgggiid. 3) Incuietori: [inc(d,0),inc(d,0),inc(i,1),inc(i,1),inc(i,2),inc(i,2),inc(d,0)]. Folosim cheia: dgggddd. 4) Incuietori: [inc(d,0),inc(d,0),inc(i,1),inc(i,1),inc(i,1),inc(i,1),inc(d,0)]. Folosim cheia: dgggddd. 5) Incuietori: [inc(d,0),inc(d,0),inc(i,1),inc(i,1),inc(d,0),inc(d,0),inc(d,0)]. Folosim cheia: gigddgg. 6) Incuietori: [inc(d,0),inc(i,1),inc(i,1),inc(d,0),inc(d,0),inc(d,0),inc(d,0)]. Folosim cheia: iddgiig. Descuierea incuietorii 2 a dus la incuierea incuietorii 6 7) Incuietori: [inc(i,1),inc(d,0),inc(d,0),inc(d,0),inc(i,1),inc(i,1),inc(i,1)]. Folosim cheia: [d,g,g,g,d,d,d] pentru a ajunge la [inc(d,0),inc(d,0),inc(d,0),inc(d,0),inc(d,0),inc(d,0),inc(d,0)]. Incuietori(stare scop): [inc(d,0),inc(d,0),inc(d,0),inc(d,0),inc(d,0),inc(d,0),inc(d,0)]

In afisare, in fata tuplului se scrie si un inc, adica inc(stare_incuietoare, numar)

Placutele colorate

Context.

Se considera o grila dreptunghiulara plasată vertical. Aceasta este impartita in locatii patratice (placute) de diverse culori (culorile vor fi notate cu cate o litera; se presupune ca nu avem mai multe culori decat litere; literele a-z sunt suficiente).

La fiecare pas se alege o zona de o anumita culoare care are cel putin K patratele in componenta sa (K≥3). Pentru a forma o astfel de zona patratelele trebuie sa fie vecine pe orizontala si verticala cu alte patratele din acea zona (nu se considera vecine si pe diagonala). Zona respectiva se elimina,si toate patratelele de deasupra ei "cad" in locurile ramase libere (nu putem avea loc liber care sa aiba deasupra patratele. In cazul in care avem o coloana libera intre patratele, coloanele din dreapta se muta la stanga, unind astfel zonele separate de coloana libera. Daca e prima coloana libera, toate coloanele se muta la stanga cu o pozitie. Coloanele libere vor fi permise doar in dreapta reprezentarii.

Scopul este sa nu mai avem patratele in grid.

De exemplu, pentru K=3 și starea: aaaa abbb cccc aaaa avem zonele: aaaa a... .... .... .... .bbb .... .... .... .... cccc .... .... .... .... aaaa

Stări și tranziții

O stare este o configurație de tablă iar tranziția reprezintă dispariția unui grup de plăcuțe. Pentru genera succesori putem alege oricare dintre zone sa fie eliminata, de exemplu, daca eliminam zona cu "c": #### aaaa abbb aaaa Acum, toate a-urile fac parte din aceeasi zona, si ar putea fi eliminate intr-un singur pas. Am notat cu # spatiile ramase vide.

Pentru starea de mai jos, daca eliminam zona de c-uri, coloanele ramase se unesc deoarece nu putem avea coloana vida. aaca abcb cccc aacc rezultatul va fi: #### aa## aba# aab#

Costul

Costul unei mutari este dat 1+(N-K)/N, unde N e numarul total de placute de culoare celor elimitate, iar K este numarul de placute eliminate in acea mutare. Cu alte cuvinte, cu cat eliminam mai multe placute cu atat costul e mai mic. De exemplu, daca din starea: aaaa abbb cccc aaaa eliminam a-urile de sus, costul va fi 1+(9-5)/9=1.44444 (alegeti voi pana la ce numar de zecimale aproximati costul).

Fisierul de intrare

Fișierul de intrare conține pe prima linie K și dedesubt matricea de plăcuțe

Pentru fisierul de intrare 3 aaaa abbb cccc aaaa

Fișier output.

Un drum din fisierul de iesire ar contine: aaaa abbb cccc aaaa #### aaaa abbb aaaa Cost mutare: 1. #### #### #### bbb# Cost mutare: 1. #### #### #### #### Cost mutare: 1. S-au realizat 3 mutari cu costul 3. Mai sus, costul fiecărei eliminări a fost 1 pentru că fiecare din ele a eliberat complet fie linii, fie coloane.

Pentru fisierul de intrare: 3 aaa abb ccc aaa Fisierul de iesire ar contine: Nu avem solutie

Lupi, capre si verze

Context

Problema se bazeaza pe jocul cunoscut cu taranul, lupul, capra si varza

Taranul vrea sa mute animalele si verzele de pe malul de est pe malul de vest. Presupuneam ca taranul nostru si-a dezvoltat afacerea, si de data asta a cumparat L lupi, C capre si V verze. Nu mai are doar o biata barca, ci un vaporas cu 2 compartimente (A si B) in care incap cate K1 si respectiv K2 elemente.

De asemenea, pe malul celalalt taranul are o magazie cu M locuri (adica, in care incap M elemente).

Atat in compartimente cat si in magazie taranul nu pune niciodata elemente de tipuri diferite (de exemplu, vor fi doar capre sau doar lupi, dar niciodata si lupi si capre). Cand taranul nu se afla impreuna cu caprele sau lupii, acestia mananca ce gasesc, mai exact: caprele mananca verze, lupii mamanca capre, si, numai cand nu au capre, alti lupi. Daca nu au ce manca, toti stau cuminti. Verzele sunt de asemenea cuminti, nu mananca pe nimeni. In magazie sau in compartimentele din barca nimeni nu va manca pe nimeni fiind mereu elemente de acelasi tip.

Barca nu pleaca fara taran, dar poate pleca cu compartimetele goale. Animalele mananca doar dupa ce a plecat barca

Starea finala e atinsa cand nu mai sunt animale pe malul initial si in plus pe malul opus sunt minim animalele cerute in fisier (de exemplu, daca se cer "3 verze 10 capre 1 lupi" este valida o solutie cu "10 verze 10 capre 1 lupi".

Stări și tranziții. Cost.

O stare e dată de o configurație (cum sunt așezate elementele pe maluri). Nu se vor considera ca noduri și stările intermediare (cât barca e pe drum). Pentru a transporta o varza în compartimentul A ne costă 1, o capră 2, un lup 3. Compartimentul B are prețuri cu 50% mai mari. Țăranul nu stă în compartimente, pentru el costă 1 un transport. Costul unei mutări e dat de suma costurilor elementelor din barcă.

Fisierul de intrare

In fisierul de intrare se vor mentiona:

pe prima linie, numerele initiale de verze, capre si lupi
pe a doua linie (numarul de locuri din compartimente A cu K1 locuri si B cu K2 locuri, numarul M de locuri din magazie)
pe a treia linie L: N1,N2 C:N3 (cat mananca un lup N1-numarul de lupi, N2-numarul de capre, N3 cat mananca o capra). De asemenea presupunem ca intai mananca caprele (din verze) si apoi lupii (din capre/lupi).
pe a 4 linie un sir de forma "Stare finala: V verze, C capre, L lupi" -reprezinta minimul de capre, verze si lupi cu care trebuie sa ramana taranul dupa ce a mutat toate entitatile de pe malul initial pe malul opus.

De exemplu avem fisierul de intrare:


20 verze 5 capre 2 lupi

3 4 5

L: 1,1 C:2

Stare finala: 14 verze 7 capre 1 lupi

Starea initiala se traduce astfel. Pe malul est se afla 20 verze, 5 capre, 2 lupi. Compartimentele din barca au A:3 si B:4 locuri. Magazia are 5 locuri. Lupii mananca fiecare cate o capra (si, respectiv, cand nu au capre, cate un lup). Dupa ce au fost mutate toate entitatile, pe malul vest trebuie sa fie minim 14 verze, 7 capre, 1 lupi.

Observatii:

se pot face si diverse optimizari, pentru a limita numarul de succesori. De exemplu: nu are sens sa punem in magazie elemente de un tip, daca pe mal nu se gasesc elemente care ar manca acel tip, sau ar fi mancate de acel tip. Din magazie scoatem elementele numai cand e nevoie (de exemplu, vrem sa manace sau sa fie mancate sau sa protejam alte elemente)
Nu e urmarita obtinerea unui numar cat mai mare de elemente, ci doar sa indeplineasca minimul cerut. Daca dintr-o stare nu mai pate fi obtinut minimul cerut, nu are sens sa o dezvoltam.
Lupii mananca lupi numai daca nu au existat capre deloc la acea iteratie (altfel nu se mananca intre ei chiar daca nu sunt suficiente capre pentru toti).
Ca sa limitam numarul de succesori (care oricum nu duc la o solutie), nu mai generam succesori pentru starile care au mai putine elemente decat minimul cerut in starea finala.
Animalele mananca doar dupa o plecare a barcii. La ultima stare nu se mai specifica pe malul opus daca animalele au mancat (fiind toate 0)
Cand avem 0 entitati in compartimente sau magazie, scriem 0 fara tipul lor, dar pe mal vom preciza daca avem 0 elemente de un anumit tip.

Fișier output.

Se va preciza la fiecare pas ce se află pe maluri, iar între nodurile din drum se va preciza cu ce încărcătură a plecat barca.

Un exemplu de drum: 1) Pe malul de est se gasesc: Taranul 21 verze 10 capre 2 lupi Pe malul de vest se gasesc: 0 verze 0 capre 0 lupi, magazie: 0 Barca pleaca de la est la vest cu container A: 3 capre, container B: 4 capre ------------------ 2) Pe malul de est se gasesc: 21 verze 3 capre 2 lupi Pe malul de vest se gasesc: Taranul 0 verze 7 capre 0 lupi, magazie: 0 Dupa ce au mancat pe malul est: 15 verze 1 capre 2 lupi Barca pleaca de la vest la est cu container A: 0, container B: 0 ------------------ 3) Pe malul de est se gasesc: Taranul 15 verze 1 capre 2 lupi Pe malul de vest se gasesc: 0 verze 7 capre 0 lupi, magazie: 0 Dupa ce au mancat pe malul vest: 0 verze 7 capre 0 lupi, magazie: 0 Barca pleaca de la est la vest cu container A: 3 verze, container B: 4 verze ------------------ 4) Pe malul de est se gasesc: 8 verze 1 capre 2 lupi Pe malul de vest se gasesc: Taranul 7 verze 2 capre 0 lupi, magazie: 5 capre Dupa ce au mancat pe malul est: 7 verze 0 capre 2 lupi Barca pleaca de la vest la est cu container A: 2 capre, container B: 0 ------------------ 5) Pe malul de est se gasesc: Taranul 7 verze 2 capre 2 lupi Pe malul de vest se gasesc: 7 verze 0 capre 0 lupi, magazie: 5 capre Dupa ce au mancat pe malul vest: 7 verze 0 capre 0 lupi, magazie: 5 capre Barca pleaca de la est la vest cu container A: 2 capre, container B: 4 verze ------------------ 6) Pe malul de est se gasesc: 3 verze 0 capre 2 lupi Pe malul de vest se gasesc: Taranul 11 verze 2 capre 0 lupi, magazie: 5 capre Dupa ce au mancat pe malul est: 2 verze 0 capre 1 lupi Barca pleaca de la vest la est cu container A: 2 capre, container B: 0 ------------------ 7) Pe malul de est se gasesc: Taranul 3 verze 2 capre 1 lupi Pe malul de vest se gasesc: 11 verze 0 capre 0 lupi, magazie: 5 capre Dupa ce au mancat pe malul vest: 11 verze 0 capre 0 lupi, magazie: 5 capre Barca pleaca de la est la vest cu container A: 3 verze, container B: 1 lupi ------------------ 8) Pe malul de est se gasesc: 0 verze 2 capre 0 lupi Pe malul de vest se gasesc: Taranul 14 verze 0 capre 1 lupi, magazie: 5 capre Dupa ce au mancat pe malul est: 0 verze 2 capre 0 lupi Barca pleaca de la vest la est cu container A: 0, container B: 0 ------------------ 9) Pe malul de est se gasesc: Taranul 0 verze 2 capre 0 lupi Pe malul de vest se gasesc: 14 verze 0 capre 1 lupi, magazie: 5 capre Dupa ce au mancat pe malul vest: 14 verze 0 capre 1 lupi, magazie: 5 capre Barca pleaca de la est la vest cu container A: 2 capre, container B: 0 ------------------ 10) Pe malul de est se gasesc: 0 verze 0 capre 0 lupi Pe malul de vest se gasesc: Taranul 14 verze 2 capre 1 lupi, magazie: 5 capre

Șoareci și pisici

Context

Într-o cameră sunt șoareci și pisici. Pisicile vor să prinđă șoarecii. Pisicile se pot muta pe linie, coloană și diagonală pe când șoarecii se pot deplasa doar pe linie și coloană. Pe hartă sunt și niște ascuzișuri. Dacă un șoarece intră într-o astfel de locație, nu mai e văzut de pisici. Într-un ascunziș poate intra maxim un șoarece. Cum orice animal trebuie să se miște pentru a obține o stare nouă, un șoarece nu poate rămâne ascuns decât peparcursul unei stări. Pentru deplasarea fiecărei pisici, se găsește șoarecele (neascuns) cel mai apropiat (în distanță euclidiană de ea), pisica apoi alege dintre toate căsuțele imediat vecine (pe linie, coloană sau diagonală) căsuța liberă cea mai apropiată de acel șoarece și se deplasează acolo. Dacă o pisică ajunge în aceeași căsuță cu un șoarece, îl mănâncă (șoarecele dispare de pe hartă). Noi trebuie să îndrumăm șoarecii astfel încât să iasă minim K din cameră. Ieșirea din cameră se face când un șoarece ajunge pe o căsuță specială din matrice, moment în care șoarecele dispare de pe hartă.

Stări și tranziții

La fiecare pas se deplasează toți șoarecii și toate pisicile. Nu vom genera noduri diferite pentru deplasarea fiecărui animal. Totuși pentru a face calculele, e nevoie de o ordine, astfel că:

în cadrul unei mutări, întâi se vor deplasa șoarecii. Șoarecii se deplasează în ordinea id-urilor lor: întâi șoarecele 0, apoi 1 etc.
După șoareci se deplasează piscile.

Se poate întâmpla ca un animal (șoarece sau pisică) să fie blocat la un moment dat (nu are căsuță liberă în niciuna dintre direcțiile de deplasare), caz în care stă pe loc.

Soarecii nu pot intra în casuțele cu obstacole

Pisicile nu pot intra în căsuțele cu obstacole, în ascunzișuri, în căsuțele de ieșire din cameră

Costul

Costul, în general, e dat de numărul de șoareci mutați (scade pe măsură ce scade numărul de șoareci). Totuși, avem și niște excepții. La o mutare în care un șoarece iese de pe hartă costul este 1. În cazul în care avem o mutare în care o pisică prinde un șoarece, costul acelei mutări e egal cu (numărul de pisici)*(numarul de șoareci)

Fisierul de intrare

Camera va fi reprezentată cu ajutorul unei hărți formate din caractere ASCII. Fișierul de intrare va conține numărul K și această hartă.

Camera are celule cu obstacole, în care nu pot intra nici șoareci și nici pisici.

Simbolurile din hartă vor fi:

"." (punct) pentru loc liber
"#" (hashtag) pentru obstacol
"@" (a rond) pentru ascunziș
"s" pentru șoarece, urmat de un indice:s0, s1, s2,...
"p" pentru pisică, urmat de un indice: p0, p1, p2,...
"S" pentru șoarece în ascunziș, urmat de un indice (egal cu indicele inițial al șoarecelui; dacă s4 a intrat în ascunziș, va fi reprezentat cu S4)
"E" pentru ieșire

Exemplu de fișier de intrare:


    3

    .   .   .   .   .   p2  E   .   .   p4 

    s3  .   .   s0  .   .   .   p9  .   .  

    .   E   .   .   #   .   .   .   .   .  

    .   .   .   #   p5  @   .   .   .   .  

    .   p10 .   #   .   .   .   s2  p0  .  

    .   .   #   .   .   .   .   .   .   .  

    E   .   s5  .   s1  @   .   #   p7  .  

    .   .   .   .   .   .   .   .   .   .  

    @   p1  .   #   .   p8  .   .   .   .  

    .   .   .   .   .   .   .   .   p3  .  

    p6  .   #   E   .   .   s4  @   .   .

Fișier output.

Elementele din matrice trebuie să fie aliniate astfel încât o coloană de matrice să depindă de cel mai lung id de șoarece sau pisică: dacă indicii nu depășesc 10, de exemplu, o coloană poate fi de 2 caractere cu un spațiu între coloane. Dacă indicii depășesc 10, atunci dimensiunea de coloană ar trebui să fie 3 ca să între tot identificatorul: de exemplu, s10.

Pentru cazul în care se întâmplă una dintre acțiunile de mai jos, se va afișa un mesaj special după afișarea hărții:

o pisică a mâncat un șoarece
un șoarece a ieșit de pe hartă
un animal nu s-a putut mișca

Exemplu de fișier de output (doar un început de drum, nu neapărat cel de cost minim):

1) . . . . . p2 E . . p4 s3 . . s0 . . . p9 . . . E . . # . . . . . . . . # p5 @ . . . . . p10 . # . . . s2 p0 . . . # . . . . . . . E . s5 . s1 @ . # p7 . . . . . . . . . . . @ p1 . # . p8 . . . . . . . . . . . . p3 . p6 . # E . . s4 @ . . 2) . . . . p2 . E . . . . . s0 . . . p9 . p4 . s3 E . p5 # . . . . . p10 . . # . @ . p0 . . . . . # . . . . . . . . # . . . . . . . E . . . . S1 . # . . . . p1 . . . . p7 . . @ . . # . . . . . . . . . . . p8 . p3 . . . p6 # E . s4 . @ . . Șoarecele s1 s-a ascuns. Pisica p0 a mâncat șoarecele s2. Pisica p1 a mâncat șoarecele s5. ...

Observație: p0 l-a mâncat pe s2, deoarece s2 s-a deplasat o poziție în sus, p1 l-a mâncat pe s5 deoarece s5 a coborât o poziție.