(Deadline: -)
Daca nu sunteti logati exercitiile nu se mai afiseaza.
Tehnici de cautare neinformata: depthfirst
Despre depthfirst
Algoritmul presupune parcurgerea unui graf pornind dintr-un nod special desemnat ca initial si parcurgand graful pana ajungem la un nod scop (solutie).
Ideea algoritmului.Algoritmul creeaza un fel de arbore de parcurgere. Ia nodul intial si spunem ca il expandeaza luand un prim succesor al acestuia. Apoi considera drept nod curent acest nod succesor adaugat in drum. La fiecare pas verifica daca nodul curent este nod-scop. Daca nu, ia si pentru el unul dintre succesorii neevalutai inca, si il adauga in drum. Procedeul se continua pana ori gasim o solutie, ori nu mai gasim un succesor viabil pentru nodul curent( de exemplu daca nu are el succesori, sau succesorii lui sunt toti in drum). In acel moment algoritmul se intoarce la nodul anterior nodului curent, si ia urmatorul succesor posibil (daca acesta exista; daca nu exista face intoarceri pana gaseste un nod cu succesori neprocesati).
Observatii:
- Spre deosebire de depth first, nu mai extinde mai multe drumuri in paralel, nivel de nivel. Drumurile oferite ca solutii nu mai sunt ordonate dupa lungime
- Arborele de parcurgere este construit "ramura de ramura" de la stanga la dreapta.
- Pe un graf infinit, algoritmul se poate bloca pe o ramura, deoarece tinde sa o construiasca pana da de o frunza.
Sa presupunem ca avem urmatorul labirint:
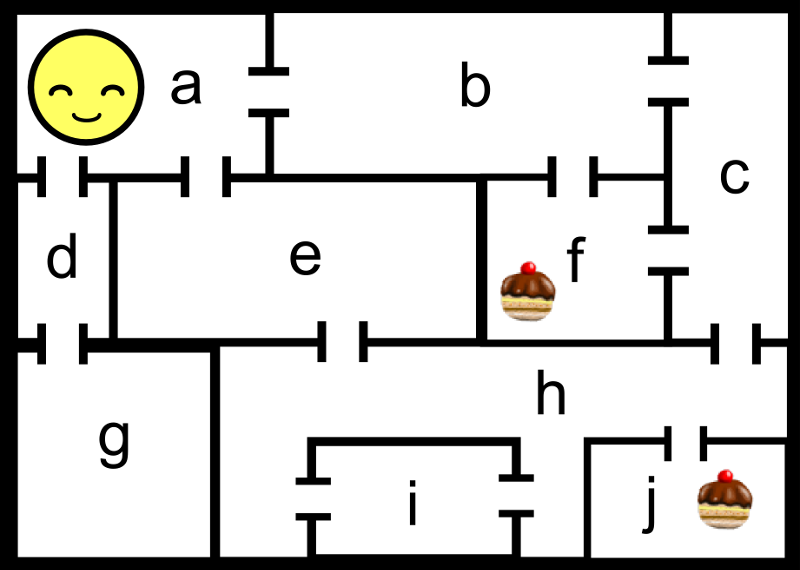
Graful asociat labirintului:
![[graful asociat camerei]](./imagini/grafAsociatCamera.png)
Arborele extinderilor se va forma in felul urmator (numai o parte din pasi):

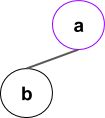
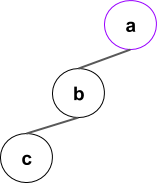
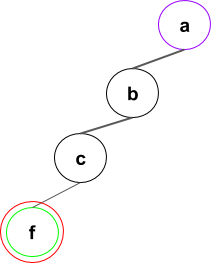
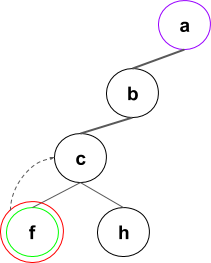
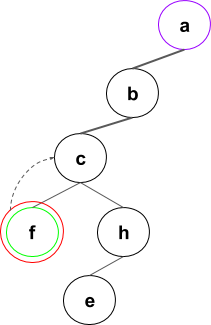
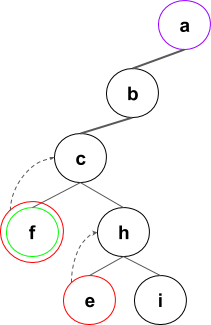
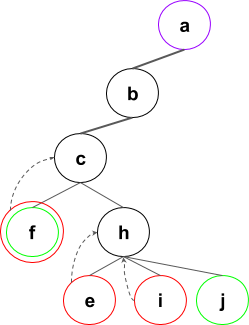
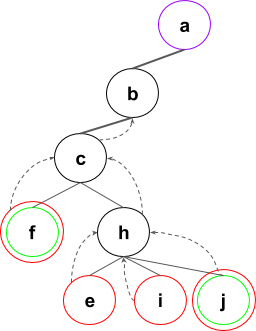
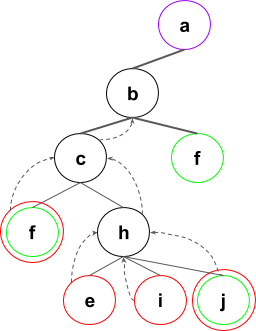
Pasii algoritmului
- Initializari. Trebuie sa stabilim un nod de start si unul sau mai multe noduri scop. Consideram o stiva S initial vida. Pentru fiecare nod din parcurgerea curenta vom memora un nod parinte (pentru a putea reconstrui drumul). Punem nodul de start in stiva S si setam nodul parinte la null (None), deoarece nodul de start e radacina arborelui de parcurgere.
- Repetam urmatorii pasi atata timp cat stiva nu e vida, sau nu ne-am oprit din cautat drumuri (am calculat deja suficiente drumuri-solutie):
- Pentru primul nod din stiva verificam daca e nod-scop, caz in care afisam drumul. Putem continua apoi algoritmul (in cazul in care avem mai multe noduri scop, putem avea un drum care se termina cu un nod-scop dar are si alte cateva astfel de noduri in componenta sa. De exemplu, drumul a, b, f, c, h, j)
- Pentru primul nod din stiva cautam un succesor care nu a mai fost evaluat pana acum din multimea de succesori ai nodului din varful stivei, si care nu se afla in stiva curenta (e nevoie si de a doua precizare fiindca nodul succesor daca se afla in stiva curenta, a fost evaluat anterior, dar cu alt parinte). Il punem in stiva, succesorul devenind astfel noul varf.
- Daca nu avem succesori pentru primul nod din stiva, il stergem din stiva (spunem ca se realizeaza o intoarcere).
Puteti descarca un exemplu de implementare in Python a tehnicii depth first.
Observatie, in cazulimplementarii date ca exemplu, nu s-a folosit efectiv o lista ca stiva. Stiva e simulata prin inlantuirea nodurilor din drum.
Tehnici de cautare neinformata: depthfirst iterative deepening (cautarea in adancime incrementala)
Despre depth-first iterative deepening
Ideea algoritmului. Se aplica algoritmul depth first pana la o adancime fixa Ad din arbore (se realizeaza o intoarcere in stiva si in momentul in care stiva are lungimea Ad, ca si cum nodul nu ar mai fi avut succesori). Iterativ, aceasta adancime creste de la 1 la o adancime maxima. Ca si in cazul depth-first-ului simplu, cand varful stivei este nod-scop, inseamna ca am gasit o solutie.
Observatii:
- Ca si la breadth first, solutiile sunt ordonate crescator dupa lungimea lor
- Arborele de parcurgere este reconstruit la fiecare nivel. Face mai multi pasi decat depth-first sau breadth-first, dar rezolva urmatoarele probleme: evita umplerea memoriei, cum se intampla la BF(coada poate creste foarte mult pentru grafuri mari), nu ramane blocat pe o ramura foarte lunga sau chiar infinita, cum se intampla la DF
Pasii algoritmului
- Initializari. Trebuie sa stabilim un nod de start si unul sau mai multe noduri scop. Stabilim si o adancime maxima, ADMAX, pana la care cautam solutii. Consideram o stiva S initial vida. Pentru fiecare nod din parcurgerea curenta vom memora un nod parinte (pentru a putea reconstrui drumul). Punem nodul de start in stiva S si setam nodul parinte la null (None), deoarece nodul de start e radacina arborelui de parcurgere.
- Pentru ADcurent(adancimea curenta) de la 1 la ADMAX aplicam algoritmul DF pe graf nemaiexpandand nodul din varful stivei daca stiva are deja lungimea Adcurent
Puteti descarca un exemplu de implementare in Python a tehnicii depth first iterative deepening.
Observatie, in cazulimplementarii date ca exemplu, nu s-a folosit efectiv o lista ca stiva. Stiva e simulata prin inlantuirea nodurilor din drum.