(Deadline: -)
Daca nu sunteti logati exercitiile nu se mai afiseaza.
Tehnici de cautare neinformata: breadthfirst
Puteti vizita wikipedia pentru a citi mai multe despre breadth-first.
Algoritmul presupune parcurgerea unui graf pornind dintr-un nod special desemnat ca initial si parcurgand graful pana ajungem la un nod scop (solutie). De exemplu: parcurgerea unui labirint (pornim dintr-o camera si incercam sa ajungem la o camera cu iesire din labirint (sau in exemplul dat, la o camera cu prajitura).
In unele situatii ne intereseaza doar sa ajungem la nodul scop fara a afisa drumul, in altele dorim sa dam ca solutie chiar drumul parcurs pana la nodul scop.
Ideea algoritmului.Algoritmul creeaza un fel de arbore de parcurgere. Ia nodul intial si spunem ca il expandeaza (adica memoreaza vecinii acestuia). Apoi ia pe rand fiecare dintre nodurile vecine astfel gasite si cauta noduri vecine si pentru ele (avand grija ca respectivele noduri sa nu mai fi fost parcurse inainte, pe acelasi drum. De exemplu un drum de forma a->b->c->a nu ar fi ales). Inainte de expandarea oricarui nod algoritmul verifica daca nodul este un nod scop.
Observatii:
- Arborele de parcurgere este construit nivel de nivel
- Algoritmul ofera cel mai scurt drum
- Algoritmul cauta solutia pe mai multe drumuri in paralel (asta nu inseamna neaparat programare paralela in sensul strict al cuvantului, ci doar faptul ca tine evidenta parcurgerii tuturor drumurilor pana la un nivelul curent in arbore).
Sa presupunem ca avem urmatorul labirint:
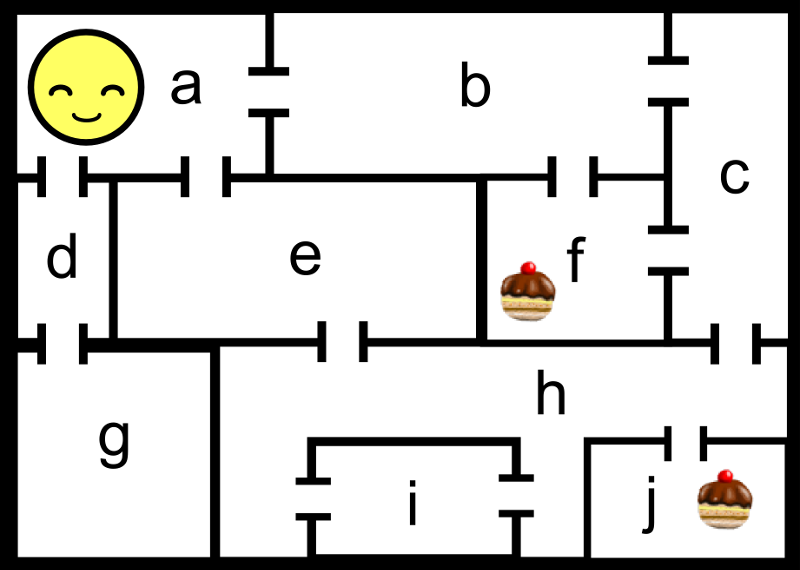
Graful asociat ar fi:
![[graful asociat camerei]](./imagini/grafAsociatCamera.png)
Arborele extinderilor se va forma in felul ilustrat mai jos. Consideram cazul in care vrem sa obtinem toate drumurile (sau oricum o parte din ele), motiv pentru care permitem inclusiv extinderea drumurilor cu noduri vizitate pe alta ramura (insa nepermitand repetarea nodului pe un drum de la radacina pana la el).
Initial avem in coada doar drumul [a]

Avem in coada: [[a,b],[a,d],[a,e]]
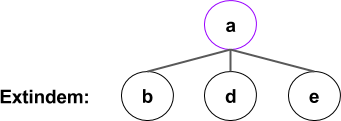
Dupa extinderea tuturor drumurilor de lungime 2:
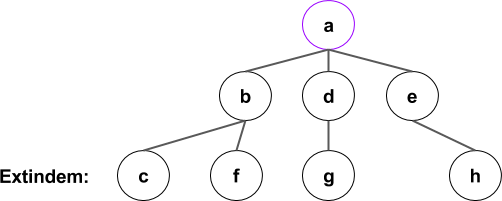
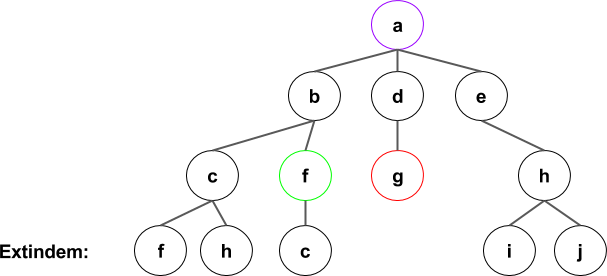
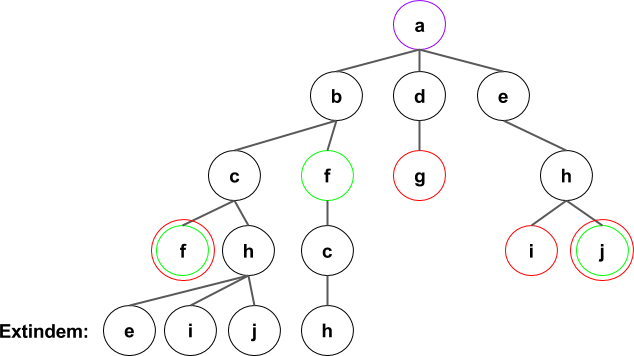
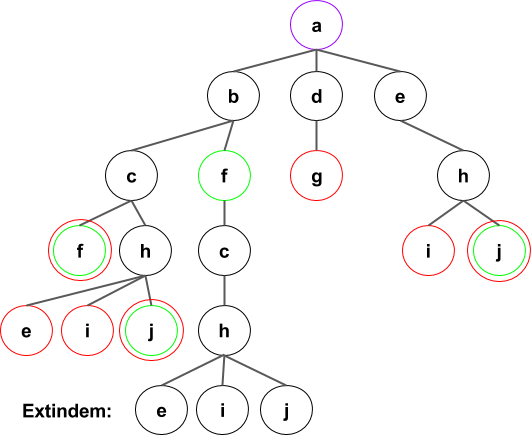
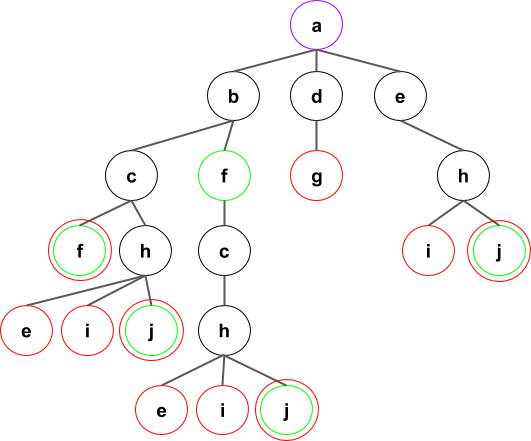
Pasii algoritmului
- Initializari. Trebuie sa stabilim un nod de start si unul sau mai multe noduri scop. In plus consideram o lista de noduri(sau drumuri, adica liste de noduri) neexpandate inca, organizata sub forma de coada (o vom nota cu c). Pentru fiecare nod vom memora un nod parinte (pentru a putea reconstrui drumul) Punem nodul de start in coada si setam nodul parinte la null (deoarece nodul de start e radacina arborelui de parcurgere).
- Repetam urmatorii pasi atata timp cat coada nu e vida, sau nu ne-am oprit din cautat drumuri (am calculat deja suficiente drumuri-solutie):
- Extragem primul nod din coada. In cazul in care memoram chiar drumuri, extragem drumul.
- Verificam daca e nod scop. Daca da, ne oprim. (in cazul in care ne intereseaza drumul in sine, afisam drumul)
- Expandam nodul extras (sau ultimul nod din drumul extras) obtinand nodurile lui vecine
- Daca nodurile nu au mai fost vizitate, le adaugam in coada c. Pentru a marca nodurile vizitate, avem doua cazuri. Daca ne intereseaza doar prima solutie, putem pur si simplu sa marcam nodul in sine ca fiind vizitat. Daca vrem sa calculam mai multe solutii, verificam pentru fiecare nod din drumul curent (de la radacina pana la nodul tocmai expandat) daca mai apare in drum, caz in care nu il adaugam in coada).
Puteti descarca un exemplu de implementare in Python a tehnicii breadth first.