Laboratory
(Deadline: 30.05.2025 00:00:00)
Daca nu sunteti logati exercitiile nu se mai afiseaza.
Morphological analysis
StanfordPOSTagger
A POS-tagger is a program that tags words in raw text, idicating their part of speech. A POS-tagger is a program that tags words in raw text, indicating their part of speech. StanfordPOSTagger is widely used in NLP tasks. Please download the full version. Unzip the archive and search for stanford-postagger.jar.
Import the tagger in python console:
from nltk.tag.stanford import StanfordPOSTagger
We want to create a tagger instance:
tagger=StanfordPOSTagger(model_path, jar_tagger_path)
To compute POS tags we use the tag() method
tagger.tag(["I","saw","a","cat"])
In case you receive an error while trying to use the tagger, read here: https://stackoverflow.com/questions/34692987/cant-make-stanford-pos-tagger-working-in-nltk
Try to parse a sentence and learn what each tag means.
Before we tag a raw text, we must tokenize it first
You can also use Stanford POStagger online version.
NLTK tagger
You can also use NLTK's own POS tagger:
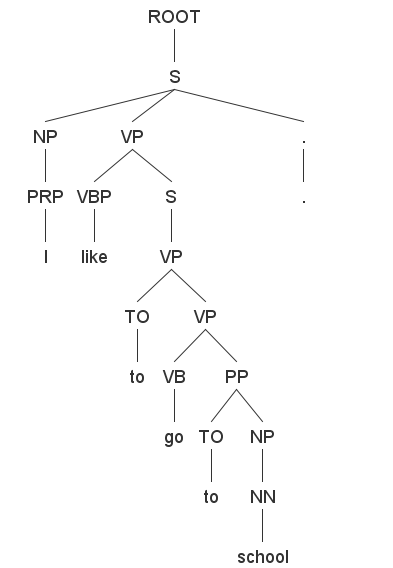
It is used to obtain the structure of the sentence and the connections between towens in a sentence. Use the graphical user interface: lexparser-gui.bat The parsing tree for this sentence:
I like to go to school.
is: This is a top-down parser, that backtracks through the rules, expanding the tree nodes in a depth-first manner. You can observe the way it works by using the app provided by nltk:
You can observe the way it works by using the app provided by nltk:
The Left-Corner Parser uses both a top-down and a bottom-up strategy. In the top-down steps it tries to predict the possible structure of the phrase, however continuosly checking the phrase structure through a bottom-up process (checking if the input phrase matches the prediction). A left-corner parser does some preprocessing before the parsing itself. It creates an association between each non-terminal label and a list of all possible left corners (start of the expression). Before applying a production from the context free grammar, it searches for the next word that there is one starting label (in the left corners list) that applies to it. Algorithm steps: We consider the following grammar (we also consider that the production rules are processed in this exact order): It is a type of chart parsing (in Romanian: parser cu agenda). It is used in order to avoi rebuilding subtrees that are already correct. All the above parsers used backtracking in their algorithm, therefore, we could have subtrees that are processed again because there is a wrong assumption in the subtrees created before them. It's in backtracking's nature to delete(forget) all the computing it made for a wrong prefix in the sollution.
Each time we build a subtree we save it in a "table" and it will be reused when it's needed.
An idea of implementation is given in the NLTK book (Natural Language Processing with Python, by Steven Bird, Ewan Klein, and Edward Loper, 2009).
Dependency Grammars (DG) are based on dependency rules between the words of a phrase. A dependency rule is between two words: the head word, and the dependent word. We will visually represent the relation between the two words in the form of an arrow, begening from the head word and ending at the dependend word. On each such arrow, the name of the dependency will also be written. The Sanford Parser prints the dependencies in a text format as you can see bellow for the phrase "I like to go to school."
nsubj(like-2, I-1) The syntax for each dependence rule is
dependency_type(head_word - position_in_sentence, dependent_word - position_in_sentence)
You can find information about the meaning dependencies at https://nlp.stanford.edu/software/stanford-dependencies.html. You can also find a list with each dependency type and its meaning at http://universaldependencies.org/u/dep/ In order to apply dependency parsing on a phrase, we'll use the Stanford parser. We'll use cmd and change the current directory to the parser directory. We also search for the models jar (the name of the file should have this syntax: stanford-parser-version-models.jar ( for example, stanford-parser-3.9.2-models.jar ) and we unzip from it the file from the relative path edu\stanford\nlp\models\lexparser\englishPCFG.ser.gz and we copy this file in the parser's folder. In cmd we write a command with this syntax:
java -mx200m -cp "stanford-parser.jar;stanford-parser-3.9.2-models.jar" edu.stanford.nlp.parser.lexparser.LexicalizedParser -retainTMPSubcategories -outputFormat "wordsAndTags,penn,typedDependencies" englishPCFG.ser.gz [path_to_input_file] > [path_to_output_file]
For the outputFormat parameter, we've specified:
In the input file you'll write the text to be parsed. It can contain multiple phrases. By default the result is printed in the console, but we can redirect the output to an output file, using ">" and specifying the output file path, for example
java -mx200m -cp "stanford-parser.jar;stanford-parser-3.9.2-models.jar" edu.stanford.nlp.parser.lexparser.LexicalizedParser -retainTMPSubcategories -outputFormat "wordsAndTags,penn,typedDependencies" englishPCFG.ser.gz ../text.txt > ../out.txt
where ../text.txt is a relative path for a file containing the text to be parsed and "../out.txt" will be the relative path to the output file for the parsing.
To easily visualise the dependencies, we download DependenSee from the extensions section, at https://nlp.stanford.edu/software/lex-parser.html. We add the jar file in the parser's folder. Use a command similar to the one bellow:
java -cp dependensee-3.7.0.jar;stanford-parser.jar;stanford-parser-3.9.2-models.jar;slf4j-api.jar com.chaoticity.dependensee.Main [fraza de parsat] [cale fisier png de output]
for example (it is the exact example from DependenSee official web page):
java -cp "dependensee-3.7.0.jar;stanford-parser.jar;stanford-parser-3.9.2-models.jar" com.chaoticity.dependensee.Main "Example isn't another way to teach, it is the only way to teach." out.png
Atention, this command is for Windows. If you are using Unix, you need the corresponding separator: use : instead of ; in classpath.. For CFG parsing: For dependency parsing: All exercises can be done by all students, unregarding attendance.
>>> nltk.pos_tag(["I", "saw", "a", "cat"])
You can find the tags meaning with:
[('I', 'PRP'), ('saw', 'VBD'), ('a', 'DT'), ('cat', 'NN')]
nltk.help.upenn_tagset(tag)
>>> nltk.help.upenn_tagset('DT')
DT: determiner
all an another any both del each either every half la many much nary
neither no some such that the them these this those
>>>
Syntax analysis
Parsing based on Context-Free Grammar
Please download the Stanford Parser.
Recursive Descent Parsing
gram=nltk.CFG.fromstring(""" S -> NP VP | TO VB
VP -> V NP | V NP PP | V S | V PP
PP -> P NP
V -> "caught" | "ate" | "likes" | "like" | "chase" | "go"
NP -> Det N | Det N PP | PRP
Det -> "the" | "a" | "an" | "my" | "some"
N -> "mice" | "cat" | "dog" | "school"
P -> "in" | "to" | "on"
TO -> "to"
PRP -> "I" """)
>>> sent=["I", "like", "my", "dog"]
>>> rdp = nltk.RecursiveDescentParser(gram)
>>> for tree in rdp.parse(sent):
print(tree)
(S (NP (PRP I)) (VP (V like) (NP (Det my) (N dog))))
nltk.app.rdparser()
Shift Reduce Parsing
>>> srp = nltk.ShiftReduceParser(gram)
>>> sent=["I", "like", "my", "dog"]
>>> for tree in srp.parse(sent):
print(tree)
(S (NP (PRP I)) (VP (V like) (NP (Det my) (N dog))))
nltk.app.srparser()
Left corner parser
S -> VP
NP -> DT NN
NP -> DT JJ NN
NP -> PRP
VP -> VBP NP
VP -> VBP VP
VP -> VBG NP
VP -> TO VP
VP -> VB
VP -> VB NP
NN -> "show" | "book"
PRP -> "|"
VBP -> "am"
VBG -> "watching"
VB -> "show"
DT -> "a" | "the"
MD -> "will"
The left corner table would be:
Symbol Left corner
S NP,VP
NP DT,PRP
VP VBP, VBG, TO, VB
NN "show", "book"
PRP "I"
VBP "am"
VBG "watching"
VB "show"
DT "a", "the"
MD "will"
Well-Formed Substring Tables
It is not mandatory to use a matrix, you can save the agenda with a list of subtrees, however you still need to save (in that structure) the indexes for the leafs contained by each subtree.
Dependency parsing
nsubj:xsubj(go-4, I-1)
root(ROOT-0, like-2)
mark(go-4, to-3)
xcomp(like-2, go-4)
case(school-6, to-5)
nmod:to(go-4, school-6)
Projective Dependency Parsing
Non-Projective Dependency Parsing
Using Stanford Parser in NLTK
from nltk.parse.stanford import StanfordParser
os.environ['JAVAHOME'] = "cale folder bin java"
os.environ['STANFORD_PARSER'] = 'cale relativa/absoluta jar parser'
os.environ['STANFORD_MODELS'] = 'cale relativa/absoluta jar modele'
parser = StanfordParser(model_path="cale relativa/absoluta englishPCFG.ser.gz")
propozitii = parser.raw_parse_sents(("I like to go to school.", "The cat is running through the room.","Where are you?"))
for prop in propozitii:
print(list(prop))
from nltk.parse.stanford import StanfordDependencyParser
# you can also use nltk.parse.corenlp.CoreNLPDependencyParser
os.environ['JAVAHOME'] = "cale folder bin java"
cale_parser = 'cale relativa/absoluta jar parser'
cale_modele = 'cale relativa/absoluta jar modele'
dependency_parser = StanfordDependencyParser(path_to_jar=cale_parser, path_to_models_jar=cale_modele)
dependente = dependency_parser.raw_parse('I like to go to school.')
for dep in dependente:
print(list(dep.triples()))
Exercises and homework