Laboratory
(Deadline: -)
Daca nu sunteti logati exercitiile nu se mai afiseaza.
Ant Colony Algorithm for the of Texts
It was developped by Didier Schwab, Jérôme Goulian, Andon Tchechmedjiev, Hervé Blanchon in their article Ant Colony Algorithm for the Unsupervised Word Sense Disambiguation of Texts: Comparison and Evaluation
Algorithm description
- Ant colony algorithm is based on the way ants search for food.
- It is a global word sense disambiguation algorithm. It is unsuppervised, meaning it needs no tagged corpora to train.
- it is an incomplete approach - it doesn't go through the entire sollution space, it tries to obtain a local maximum
- The context window for the analysis will be the whole text.
- It uses a modified extended Lesk measure
Ant colony algorithms
They are part of the swarm intelligence algorithms cathegory
The problem is usually represented as a graph, and the ants walk through this graph in search for food and back to their nests. The graph has two types of nodes:
- common nodes
- nests
The nests are ants generators. The ants start searching for energy (food) throughout the graph. The number of ants produced by the nest depends on how much energy the nest has (if it has more energy (brought by the ants), it can produce more ants).
When ants walk on an edge they leave an odour tray corresponding to their mother nest. The odour will help other to adjust their routes.
An ant sees the nodes in the algorithm in three possible ways:
- mother nest (where it was produced)
- enemy nest (rivals to the mother nest)
- potential friend nest (the rest of the nests)
Ants choose to follow a certain edge depending on the found pheromone on the edge, on the odour of other nodes and on the energy
Ants can create bridges (new edges) between nests based on a computed score between them. However, these bridges disappear if they reach 0 pheromone.
Implementation steps
We will use the same notations that were used in the article:
| Notation | Meaning |
|---|---|
| wi | a word (i is an index) |
| wi, j | a sense j for the word i |
| d(wi, j) | the definition for the sense j of the word i |
| C | a configuration of senses (a potential soluution) organized as a list of senses corresponding to ech word from the text |
- Create a function that computes the relatedness between two senses, based on the Extended Lesk measure, but with the following modification: you will not take into consideration the postion of the words (we don't compute the common substrings, just the number of common words, like in the original Lesk algorithm). Stop words must be eliminated from the definition. You consider the whole definition text as a bag of words. To compute this measure (and also to use the definitions further in the algorithm) we assign a number (like an id) to each definition word (from all the definitions) and we sort the resulting set of numbers. For example, for the definition:
>>> from nltk.corpus import wordnetLet's imagine that we have the following assignments:
>>> wordnet.synset('flower.n.01').definition()
'a plant cultivated for its blooms or blossoms'
>>> from nltk.corpus import stopwords
>>> l=wordnet.synset('flower.n.01').definition().split(' ')
>>> l
['a', 'plant', 'cultivated', 'for', 'its', 'blooms', 'or', 'blossoms']
>>> [x for x in l if x not in stopwords.words('english')]
['plant', 'cultivated', 'blooms', 'blossoms']- plant - 7
- cultivated - 1
- blooms - 55
- blossoms - 23
- we create a fitness function that computes the score for a configuration (a list of assigned sesnes for the words in the text):
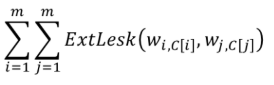
C[k] is the assigned sense for the word in k-th position in the text - We create the correspondin problem graph:
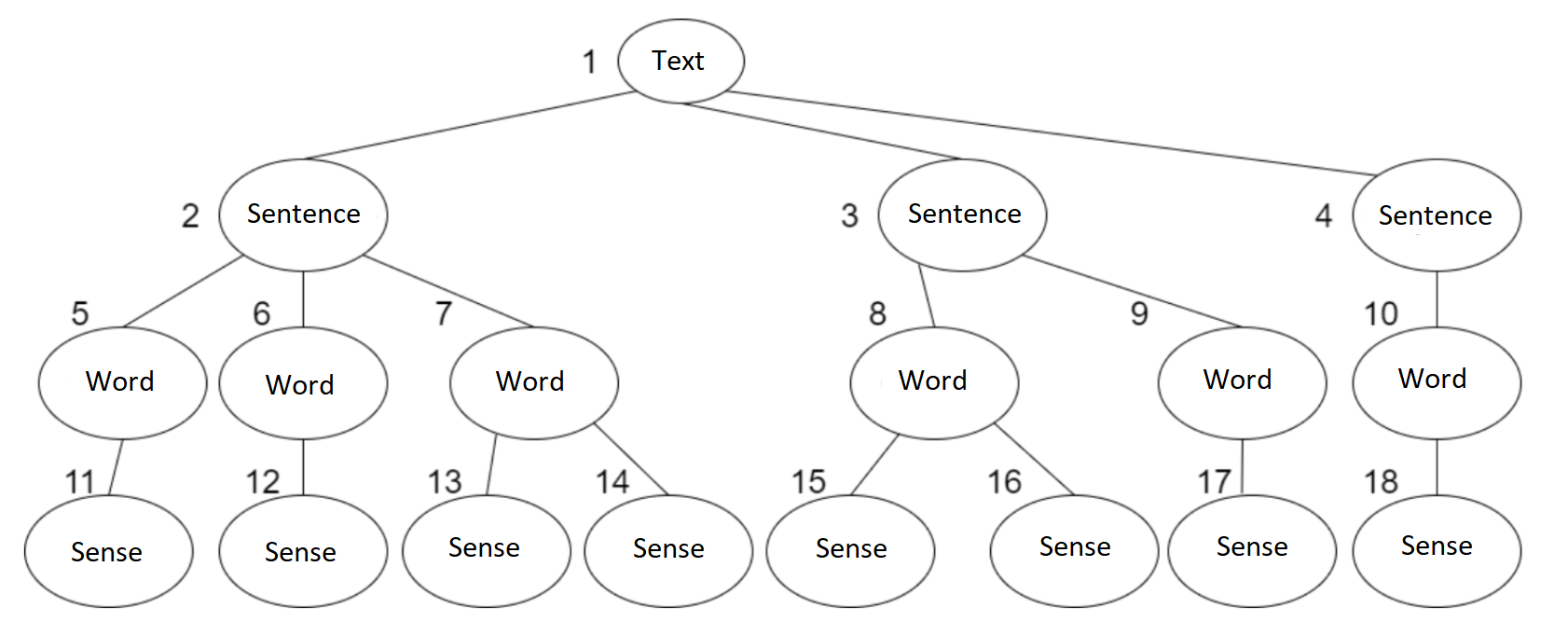
The word senses are the nests, and the rest of the nodes are common nodes. Each node has assigned an initial energy (in the article they used values between 5-60) - We assign the initial odour to the nodes in the graph. The odour will be represented by an array of a fixed length (in the article they used a length between 20-200). The nests have the words in the definition in their odour array. Common nodes have (initially) null values in their odour array.
- The algorithm will run on a certain number of cycles (the maximum number of cycles used in the algorithm was 500) that contain three actions:
- clean the graph by removing the dead ants (ants have a lifespan of ω cycles; in the article they set ω to a fixed number between 1-30;). The energy that was carried by the ant is added to the energy of the node where it died. We also remove the bridges with zero pheromone
- produce new ants. The ants are produced with a certain probability coputed through this formula: arctan(E(N))/π+0.5, where E(N) is the energy in the nest node N.
- move the ants in the graph and create bridges if the move requires so. The ant when searching for energy chooses an edge to move with the following probability:
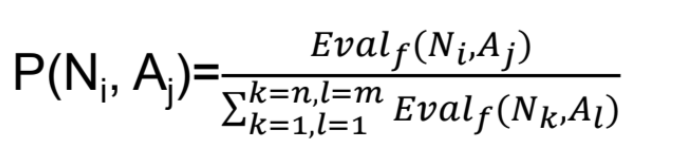
Evalf(N,A)=Evalf(N)+Evalf(A)
Evalf(A) = 1 − φt(A)
φt(A)= quantity of pheromone on edge A
.png)
An ant decides to return with the probability E(f)/Emax It uses the same probability Evalf(N,A) with Evalf(A) = φt(A)
and
_return.png)
When creating a bridge, we have Evalf(A)=0 - compute the new energy and odour for the nodes, and the pheromone on the edges. For each passing an ant deposits some pheromone on that edge(new_pheromone =old_pheromone+θ). Also we have an evaporation rate, 𝛿 (on an edge new_pheromone= old_pheromone*(1-𝛿). An ant randomly gives parts of its odour to the node it travels through.
- we choose the senses corresponding to the nest with the highest amount of energy
- Observation: Bridges between unrelated senses will disappear in time (because the pheromone is dissipated in time), however, bridges between related senses will thrive.
Exercises and homework
All exercises can be done by all students, unregarding attendance.